Pewne przedsiębiorstwo postanowiło przyznać każdemu pracownikowi losowy 5-cyfrowy identyfikator, przy czym ustalono, że w identyfikatorze nie może występować cyfra 0. Prawdopodobieństwo 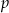 otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
A) 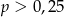 B)
B) 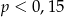 C)
C) 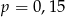 D)
D) 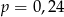
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Różne
Mamy dwie urny. W pierwszej są 3 kule białe i 7 kul czarnych, w drugiej jest jedna kula biała i 9 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z jednym oczkiem, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 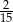 B)
B) 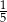 C)
C) 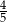 D)
D) 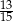
Mamy dwie urny. W pierwszej jest 5 kul białych i 5 kul czarnych, w drugiej są 3 kule białe i 7 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z liczbą oczek podzielną przez 3, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 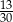 B)
B) 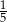 C)
C) 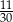 D)
D) 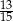
W pudełku znajdują się płytki z literami i cyframi. Na każdej płytce jest wydrukowana albo jedna wielka litera, albo jedna mała litera, albo jedna cyfra. Płytek z wielkimi literami jest o 25% mniej niż płytek z cyframi, a płytek z małymi literami jest o 40% więcej niż płytek z wielkimi literami. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z cyfrą jest równe
A) 0,85 B) 0,1 C) 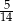 D)
D) 
Doświadczenie losowe polega na rzucie trzema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że liczba oczek otrzymanych na kostce jest równa liczbie wylosowanych orłów na monetach jest równe
A) 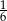 B)
B) 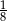 C)
C) 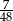 D)
D) 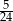
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 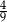 D)
D) 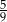
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 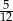 C)
C) 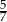 D) 0,4
D) 0,4
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 1 B) 2 C) 100 D) 6
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się tysiąckrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 3 B) 2 C) 1000 D) 7
Kod dostępu do sejfu składa się z pięciu cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile cyfr powinien mieć nowy kod?
A) 7 B) 2 C) 100 D) 6
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
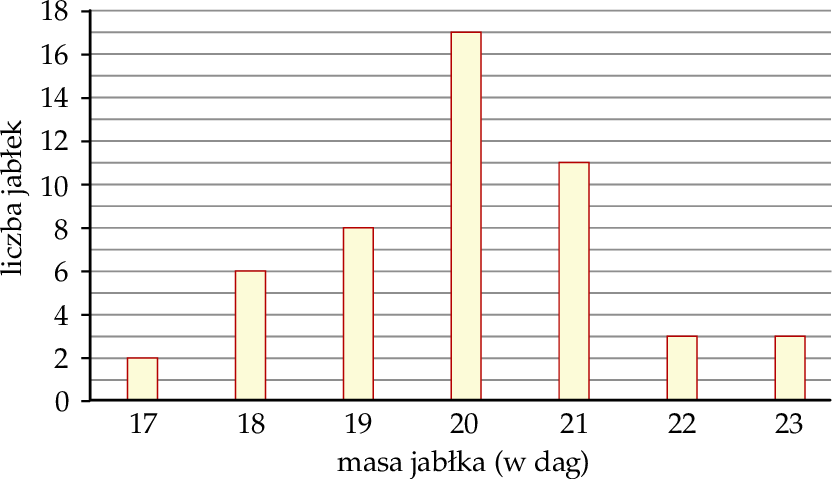
Spośród 50 zważonych jabłek z pobranej próby kontrolnej losujemy jedno jabłko. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane jabłko spełnia normę jakości, jest równe
A)  B)
B)  C)
C) 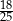 D)
D) 
W hurtowni owoców wyselekcjonowana gruszka spełnia normę jakości, gdy jej masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [16 dag, 18 dag]. Pobrano próbę kontrolną liczącą 50 gruszek i następnie zważono każdą z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy gruszek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę gruszki (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę gruszek o określonej masie.
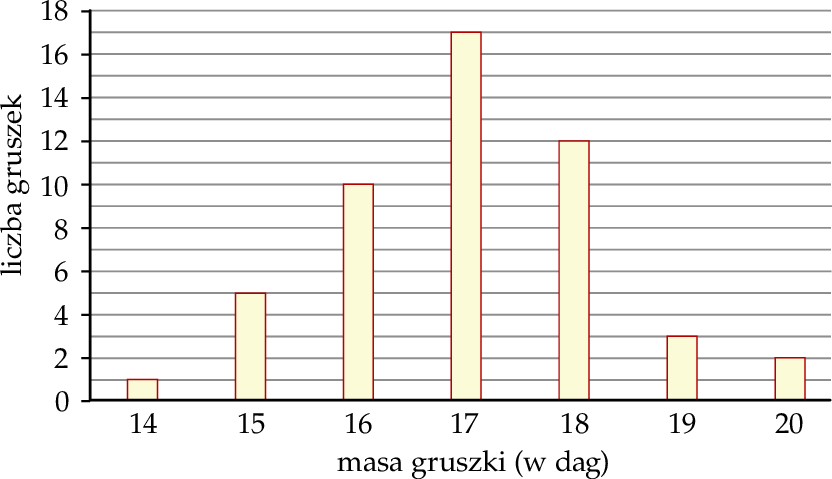
Spośród 50 zważonych gruszek z pobranej próby kontrolnej losujemy jedną gruszkę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana gruszka spełnia normę jakości, jest równe
A) 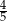 B)
B) 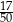 C)
C) 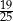 D)
D) 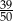
Mamy cztery urny. W urnie o numerze 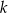 , dla
, dla 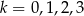 znajduje się
znajduje się 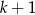 kul białych i
kul białych i 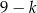 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z 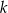 oczkami,
oczkami, 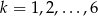 to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby
to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby 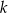 przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 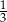 B)
B) 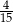 C)
C) 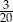 D)
D) 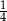
W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
A) 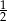 B)
B) 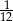 C)
C) 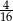 D)
D) 
W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo wyciągnięcia z woreczka piłki szarej jest równe
A) 0,75 B) 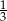 C) 0,25 D) 0,8
C) 0,25 D) 0,8
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 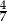 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A)  B) 0,75 C)
B) 0,75 C)  D)
D) 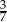
W szufladzie jest 40 koszulek, wśród których 10% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 35 koszulek, wśród których 20% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 50 koszulek, wśród których 30% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będzie co najmniej pięć koszulek niebieskich?
A) 20 B) 10 C) 7 D) 3
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu są dwa orły i sześć oczek na kostce, jest równe
A) 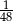 B)
B) 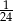 C)
C) 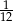 D)
D) 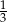
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu jest co najmniej jedna reszka i trzy oczka na kostce, jest równe
A) 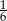 B)
B) 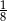 C)
C) 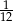 D)
D) 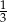
Jacek bierze udział w olimpiadzie chemicznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady chemicznej jest równe 0,3, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,72. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,1 B) 0,6 C) 0,7 D) 0,4
Ania bierze udział w olimpiadzie biologicznej i olimpiadzie fizycznej. Prawdopodobieństwo, że zostanie laureatką olimpiady biologicznej jest równe 0,4, a prawdopodobieństwo, że zostanie laureatką przynajmniej jednej z tych dwóch olimpiad wynosi 0,62. Prawdopodobieństwo, że będzie laureatką obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatką olimpiady fizycznej jest równe
A) 0,4 B) 0,3 C) 0,5 D) 0,2
Tomek bierze udział w olimpiadzie fizycznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady fizycznej jest równe 0,5, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,74. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,26. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,5 B) 0,6 C) 0,7 D) 0,4
Jacek i Karol rzucają śnieżkami do celu. Jacek trafia do celu średnio trzy razy na dziesięć rzutów, a Karol trafia do celu średnio raz na pięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każdy z chłopców wykona po jednym rzucie jest równe
A) 0,06 B) 0,38 C) 0,56 D) 0,5
Ewa i Kasia rzucają śnieżkami do celu. Ewa trafia do celu średnio raz na pięć rzutów, a Kasia trafia do celu średnio trzy razy na dziesięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każda z dziewcząt wykona po jednym rzucie jest równe
A) 0,5 B) 0,56 C) 0,38 D) 0,06

