Rzucamy trzy razy symetryczną monetą. Niech 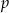 oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A) 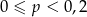 B)
B) 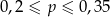 C)
C) 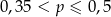 D)
D) 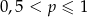
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Monety i banknoty
Rzucamy trzy razy symetryczną monetą. Niech 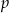 oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
A) 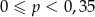 B)
B) 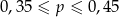 C)
C) 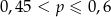 D)
D) 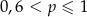
Rzucamy trzy razy symetryczną monetą. Niech 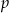 oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
A) 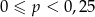 B)
B) 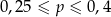 C)
C) 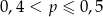 D)
D) 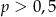
Rzucamy dziewięć razy symetryczną monetą. Niech 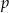 oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
A) 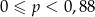 B)
B) 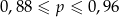 C)
C) 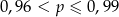 D)
D) 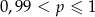
Rzucamy trzy razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednej reszki jest równe
A)  B)
B) 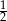 C)
C) 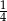 D)
D) 
Rzucamy cztery razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednego orła jest równe
A)  B)
B) 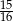 C)
C) 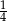 D)
D) 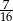
Rzucamy 10 razy symetryczną monetą. Niech 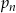 dla
dla 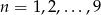 oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach
oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach  i
i 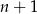 . Wtedy
. Wtedy
A) 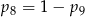 B)
B) 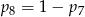 C)
C) 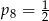 D)
D) 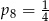
Prawdopodobieństwo, że w trzykrotnym rzucie symetryczną monetą otrzymamy dwa orły i jedną reszkę, jest równe
A)  B) 0,5 C) 0,375 D)
B) 0,5 C) 0,375 D) 
Prawdopodobieństwo, że w czterokrotnym rzucie symetryczną monetą otrzymamy trzy reszki i jednego orła, jest równe
A)  B) 0,375 C) 0,25 D)
B) 0,375 C) 0,25 D) 
Prawdopodobieństwo, że w czterokrotnym rzucie symetryczną monetą otrzymamy trzy orły i jedną reszkę, jest równe
A)  B) 0,25 C) 0,375 D)
B) 0,25 C) 0,375 D) 
Doświadczenie losowe polega na trzykrotnym rzucie monetą. Prawdopodobieństwo, że dokładnie dwa razy wylosujemy orła wynosi
A)  B)
B) 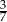 C)
C)  D)
D) 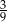
Rzucamy trzykrotnie symetryczną monetą. Prawdopodobieństwo, że w trzecim rzucie wypadnie orzeł jest równe
A) 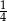 B)
B)  C)
C) 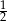 D)
D) 
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwa orły jest równe
A) 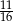 B)
B)  C)
C) 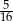 D)
D) 
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwie reszki jest równe
A) 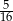 B)
B) 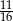 C)
C)  D)
D) 
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy orły, jest równe
A) 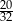 B)
B) 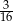 C)
C) 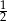 D)
D) 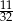
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najwyżej 2 reszki, jest równe
A) 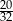 B)
B) 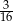 C)
C) 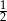 D)
D) 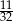
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy reszki, jest równe
A) 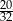 B)
B) 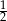 C)
C) 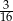 D)
D) 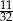
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 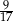 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 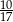 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 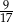 B)
B) 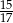 C)
C) 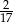 D)
D)