Wielomian 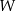 określony wzorem
określony wzorem 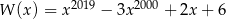
A) jest podzielny przez 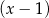 i z dzielenia przez
i z dzielenia przez 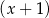 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 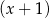 i z dzielenia przez
i z dzielenia przez 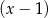 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 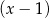 i jest podzielny przez
i jest podzielny przez 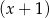 .
.
D) nie jest podzielny ani przez 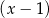 , ani przez
, ani przez 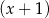 .
.
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Jeden wielomian/Różne
Wielomian 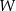 określony wzorem
określony wzorem 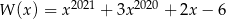
A) jest podzielny przez 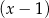 i z dzielenia przez
i z dzielenia przez 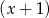 daje resztę równą
daje resztę równą 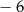 .
.
B) jest podzielny przez 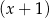 i z dzielenia przez
i z dzielenia przez 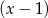 daje resztę równą
daje resztę równą 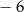 .
.
C) jest podzielny przez 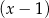 i jest podzielny przez
i jest podzielny przez 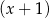 .
.
D) nie jest podzielny ani przez 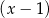 , ani przez
, ani przez 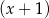 .
.
Wiadomo, że wśród pierwiastków wielomianu 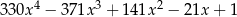 są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
A) 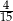 B)
B) 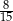 C)
C) 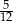 D)
D) 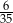
Wiadomo, że wielomian 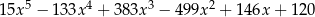 ma w zbiorze
ma w zbiorze 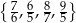 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 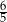 B)
B)  C)
C) 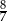 D)
D) 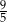
Wiadomo, że wielomian 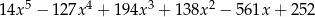 ma w zbiorze
ma w zbiorze 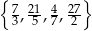 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A)  B)
B) 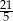 C)
C) 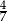 D)
D) 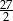
Dany jest wielomian 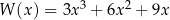 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wielomian 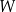 jest iloczynem wielomianów jest iloczynem wielomianów 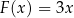 i i 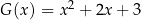 . . | P | F |
Liczba 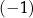 jest rozwiązaniem równania jest rozwiązaniem równania 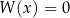 . . | P | F |
Największa wartość funkcji 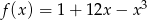
A) jest równa 17 B) jest równa 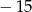 C) jest równa 4 D) nie istnieje
C) jest równa 4 D) nie istnieje
Wielomian 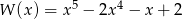
A) jest iloczynem wielomianów 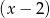 i
i 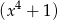
B) ma trzy miejsca zerowe
C) ma dwa miejsca zerowe
D) jest różnicą wielomianów 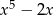 i
i 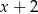
Wielomian 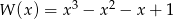
A) jest różnicą wielomianów 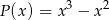 oraz
oraz 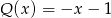
B) nie ma pierwiastków
C) ma jeden pierwiastek
D) dla argumentu 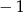 przyjmuje wartość zero
przyjmuje wartość zero
Wielomian 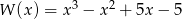
A) jest różnicą wielomianów 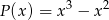 oraz
oraz 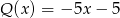
B) ma trzy pierwiastki
C) ma jeden pierwiastek
D) dla argumentu 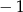 przyjmuje wartość zero
przyjmuje wartość zero
Wielomian 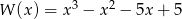
A) jest różnicą wielomianów 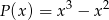 oraz
oraz 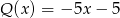
B) dla argumentu 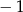 przyjmuje wartość zero
przyjmuje wartość zero
C) ma jeden pierwiastek
D) ma trzy pierwiastki
Wielomian 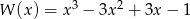
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 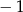 przyjmuje wartość
przyjmuje wartość 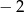
C) wartość równą 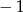 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 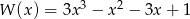
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 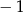 przyjmuje wartość
przyjmuje wartość 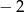
C) wartość równą 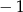 przyjmuje dla czterech argumentów
przyjmuje dla czterech argumentów
D) ma trzy różne pierwiastki
Wielomian 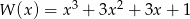
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 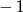 przyjmuje wartość
przyjmuje wartość 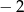
C) wartość równą 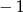 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 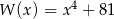 jest podzielny przez
jest podzielny przez
A) 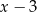 B)
B) 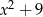 C)
C)  D)
D) 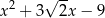
Wielomian 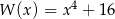 jest podzielny przez
jest podzielny przez
A) 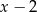 B)
B) 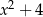 C)
C) 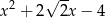 D)
D) 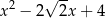
Wielomian 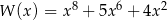 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 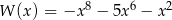 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 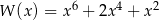 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie B) wartości nieujemne
C) tylko wartości ujemne D) tylko wartości dodatnie

