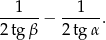W trójkącie ostrokątnym 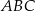 bok
bok 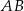 ma długość
ma długość  , długość boku
, długość boku 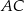 jest równa
jest równa 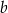 oraz
oraz 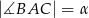 . Dwusieczna kąta
. Dwusieczna kąta 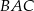 przecina bok
przecina bok 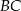 trójkąta w punkcie
trójkąta w punkcie 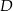 i odcinek
i odcinek 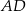 ma długość
ma długość 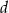 . Wykaż, że
. Wykaż, że
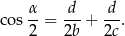
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie ostrokątnym 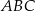 bok
bok 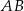 ma długość
ma długość  , długość boku
, długość boku 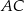 jest równa
jest równa 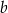 oraz
oraz 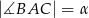 . Dwusieczna kąta
. Dwusieczna kąta 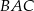 przecina bok
przecina bok 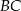 trójkąta w punkcie
trójkąta w punkcie 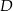 i odcinek
i odcinek 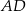 ma długość
ma długość 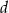 . Wykaż, że
. Wykaż, że
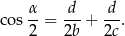
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 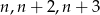 jest rozwartokątny.
jest rozwartokątny.
Dany jest trójkąt 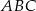 , w którym
, w którym 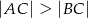 . Na bokach
. Na bokach 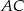 i
i 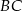 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 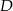 i
i 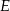 , że zachodzi równość
, że zachodzi równość 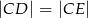 . Proste
. Proste 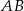 i
i 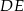 przecinają się w punkcie
przecinają się w punkcie 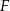 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 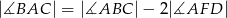 .
.
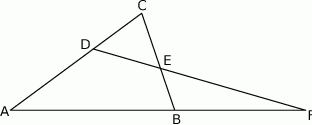
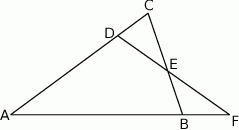
Dany jest trójkąt 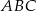 , w którym
, w którym 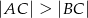 . Na bokach
. Na bokach 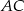 i
i 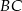 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 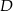 i
i 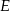 , że zachodzi równość
, że zachodzi równość 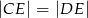 . Proste
. Proste 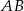 i
i 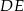 przecinają się w punkcie
przecinają się w punkcie 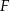 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 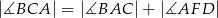 .
.
Wykaż, że jeśli 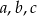 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 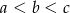 oraz
oraz 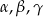 są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków 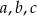 , to
, to 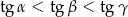 .
.
Wykaż, że jeżeli w trójkącie 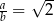 to
to 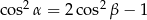 .
.
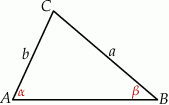
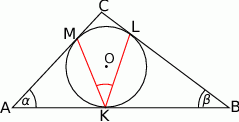
W trójkąt 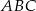 , w którym
, w którym 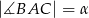 oraz
oraz 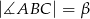 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 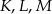 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 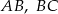 i
i 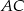 . Wykaż, że
. Wykaż, że 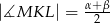 .
.
Wykaż, że jeżeli 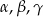 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 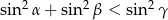 , to
, to 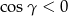 .
.
Wykaż, że jeżeli 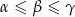 są kątami wewnętrznymi trójkąta rozwartokątnego, to
są kątami wewnętrznymi trójkąta rozwartokątnego, to
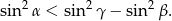
Wierzchołek 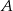 trójkąta ostrokątnego
trójkąta ostrokątnego 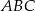 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 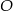 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 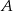 poprowadzono wysokość
poprowadzono wysokość 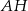 . Wykaż, że
. Wykaż, że 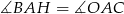 .
.
Trójkąt 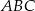 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 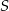 . Kąty wewnętrzne
. Kąty wewnętrzne 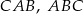 i
i 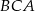 tego trójkąta są równe, odpowiednio,
tego trójkąta są równe, odpowiednio, 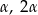 i
i 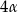 . Wykaż, że trójkąt
. Wykaż, że trójkąt 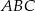 jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych
jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych 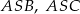 i
i 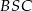 tworzą w podanej kolejności ciąg arytmetyczny.
tworzą w podanej kolejności ciąg arytmetyczny.
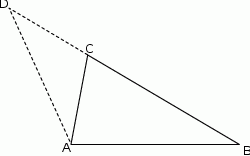
W trójkącie 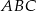 przedłużono bok
przedłużono bok 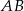 poza wierzchołek
poza wierzchołek 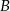 i odłożono odcinek
i odłożono odcinek 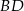 taki, że
taki, że 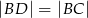 . Następnie połączono punkty
. Następnie połączono punkty 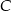 i
i 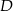 (rysunek). Wykaż, że
(rysunek). Wykaż, że 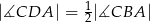 .
.
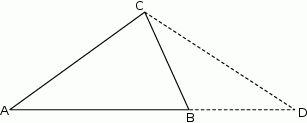
W trójkącie 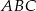 przedłużono bok
przedłużono bok 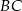 poza wierzchołek
poza wierzchołek 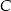 i odłożono odcinek
i odłożono odcinek 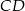 taki, że
taki, że 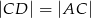 . Następnie połączono punkty
. Następnie połączono punkty 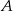 i
i 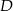 (rysunek). Wykaż, że
(rysunek). Wykaż, że 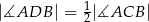 .
.
Wykaż, że jeżeli 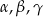 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 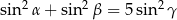 , to
, to 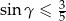 .
.
W trójkącie 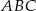 poprowadzono dwusieczne kątów
poprowadzono dwusieczne kątów 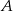 i
i 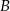 . Dwusieczne te przecinają się w punkcie
. Dwusieczne te przecinają się w punkcie 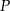 . Uzasadnij, że kąt
. Uzasadnij, że kąt 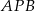 jest rozwarty.
jest rozwarty.
W trójkącie ostrokątnym 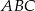 proste
proste 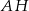 i
i 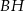 zawierają wysokości poprowadzone z wierzchołków
zawierają wysokości poprowadzone z wierzchołków 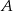 i
i 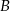 . Uzasadnij, że kąt
. Uzasadnij, że kąt 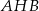 jest rozwarty.
jest rozwarty.
Okrąg wpisany w trójkąt 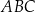 jest styczny do boków
jest styczny do boków 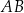 i
i 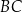 w punktach
w punktach 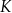 i
i 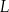 odpowiednio. Na bokach
odpowiednio. Na bokach 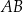 i
i 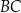 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 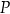 i
i 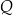 w ten sposób, że odcinek
w ten sposób, że odcinek 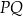 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 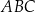 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 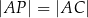 ,
, 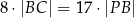 i
i 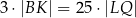 , to trójkąt
, to trójkąt 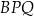 jest rozwartokątny.
jest rozwartokątny.
W trójkącie ostrokątnym 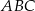 prawdziwa jest równość
prawdziwa jest równość 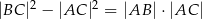 . Wykaż, że kąt
. Wykaż, że kąt 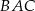 jest dwa razy większy od kąta
jest dwa razy większy od kąta 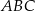 .
.
Wykaż, że jeżeli 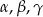 są kątami trójkąta, to
są kątami trójkąta, to
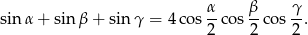
Wykaż, że jeśli 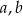 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 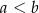 oraz
oraz 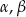 są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków 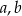 , to
, to 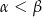 .
.
Wykaż, że jeżeli 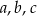 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 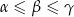 to
to 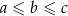 .
.
Każdy kąt trójkąta 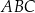 ma miarę mniejszą niż
ma miarę mniejszą niż 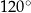 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 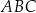 istnieje punkt
istnieje punkt 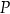 taki, że
taki, że
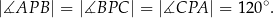
Punkt 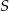 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 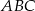 . Wykaż, że jeżeli
. Wykaż, że jeżeli 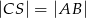 to
to 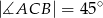 .
.
W trójkącie ostrokątnym 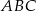 dane są
dane są 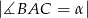 i
i 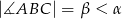 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 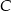 jest równy
jest równy