Oblicz długość/Równoległobok - zadania z matematyki

/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Oblicz długość

Kąt ostry między przekątnymi równoległoboku 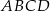ABCD ma miarę 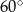∘ 60 . Przekątna 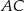ma długość 6, a przekątna 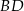jest prostopadła do boku 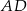. Oblicz długości boków równoległoboku.

Długości boków równoległoboku 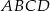ABCD wynoszą 1 i 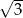√ -- 3 , a kąt przy wierzchołku 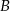ma miarę 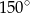150∘ . Oblicz promień okręgu opisanego na trójkącie ABD .

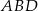Długości boków równoległoboku są równe 6 i 10, a jego pole wynosi 36. Oblicz długości przekątnych tego równoległoboku.

Ukryj Podobne zadania

Długości boków równoległoboku są równe 13 i 21, a jego pole wynosi 252. Oblicz długości przekątnych tego równoległoboku.

Dany jest równoległobok, którego obwód jest równy 50 cm. Stosunek długości jego wysokości wynosi 2:3, a stosunek miar jego kątów wewnętrznych jest równy 1:2. Oblicz długości boków i wysokości tego równoległoboku.

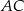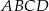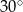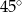Przekątna równoległoboku ABCD tworzy z jego bokami kąty o miarach 30 ∘ i 45∘ . Oblicz stosunek 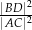2 |BD|2 |AC| kwadratów długości przekątnych tego równoległoboku.

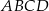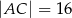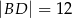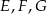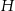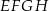Przekątne równoległoboku ABCD mają długości: |AC | = 1 6 oraz |BD | = 12 . Wierzchołki E,F,G oraz rombu EF GH leżą na bokach równoległoboku 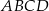ABCD (zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.

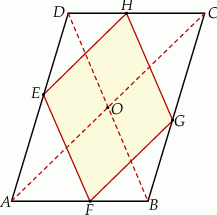
Oblicz długość boku rombu 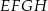EF GH .

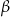Krótsza przekątna równoległoboku tworzy bokami kąty i . Oblicz stosunek długości boków tego równoległoboku.

W równoległoboku 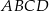ABCD miara kąta ostrego jest równa 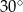∘ 30 , a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i 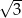√ -- 3 . Oblicz długość krótszej przekątnej tego równoległoboku.

Obwód równoległoboku 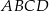ABCD jest równy 26, miara jego kąta rozwartego 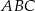ABC jest równa 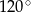120∘ , a promień okręgu wpisanego w trójkąt 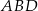ABD jest równy 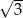√ -- 3 . Oblicz długości boków równoległoboku ABCD .

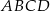Pole równoległoboku jest równe 24. Stosunek jego wysokości jest równy 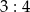3 : 4 . Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.

W równoległoboku o obwodzie równym 144, wysokośc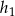i i 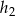spełniają warunek 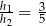hh1 = 35 2 . Oblicz długości boków tego równoległoboku.

Ukryj Podobne zadania

W równoległoboku o obwodzie równym 96 cm stosunek wysokości jest równy 5:7. Oblicz długości boków tego równoległoboku.

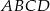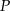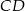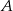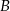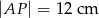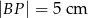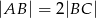W równoległoboku ABCD środek boku połączono odcinkami z wierzchołkami i . Wiadomo, że |AP | = 12 cm i |BP | = 5 cm oraz |AB | = 2|BC | . Oblicz obwód równoległoboku.

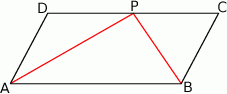
W równoległoboku ABCD przekątna 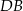ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26, 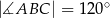|∡ABC | = 12 0∘ , oblicz długości boków równoległoboku.

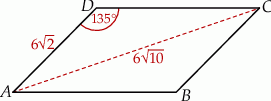
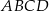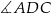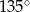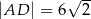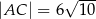Dany jest równoległobok ABCD , w którym kąt rozwarty ∡ADC ma miarę 13 5∘ . Ponadto wiadomo, że √ -- |AD | = 6 2 i √ --- |AC | = 6 1 0 (zobacz rysunek). Oblicz obwód tego równoległoboku.

W równoległoboku, w którym boki mają długości 1 i 3, symetralna krótszego boku przechodzi przez wierzchołek równoległoboku. Znajdź długości przekątnych tego równoległoboku.

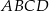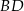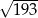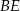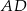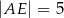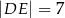W równoległoboku ABCD przekątna ma długość √ ---- 19 3 , a wysokość dzieli bok na odcinki o długościach |AE | = 5 i |DE | = 7 (zobacz rysunek).

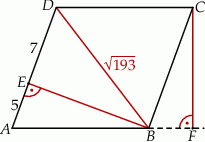
Oblicz długość wysokości 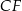tego równoległoboku.