Dany jest kwadrat 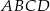 o boku długości 8. Z wierzchołka
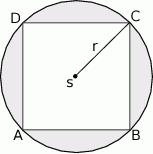
o boku długości 8. Z wierzchołka 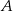 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
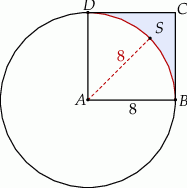
Oblicz pole powierzchni obszaru 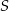 otrzymanego z kwadratu
otrzymanego z kwadratu 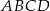 przez wycięcie części pokrytej kołem.
przez wycięcie części pokrytej kołem.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest kwadrat 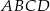 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka 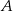 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).

Oblicz pole powierzchni obszaru 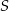 otrzymanego z kwadratu
otrzymanego z kwadratu 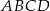 przez wycięcie części pokrytej kołem.
przez wycięcie części pokrytej kołem.
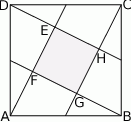
Na rysunku przedstawiono kwadrat 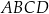 o polu 4.
o polu 4.

Punkty 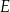 i
i 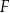 są środkami boków
są środkami boków 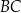 i
i 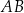 , a punkt
, a punkt 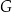 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 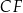 i
i 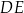 . Oblicz pole czworokąta
. Oblicz pole czworokąta 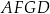
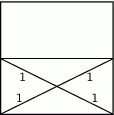
W kwadracie połączono odcinkiem środki przeciwległych boków. Wiedząc, że przekątne tak utworzonych prostokątów dzielą się na odcinki długości 1, oblicz pole wyjściowego kwadratu.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
Na kwadracie 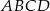 opisano okrąg o promieniu
opisano okrąg o promieniu 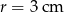 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
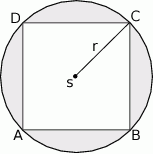
Na kwadracie  opisano okrąg o promieniu
opisano okrąg o promieniu 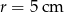 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Kwadrat 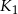 ma bok długości
ma bok długości  . Obok niego rysujemy kolejno kwadraty
. Obok niego rysujemy kolejno kwadraty 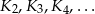 takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
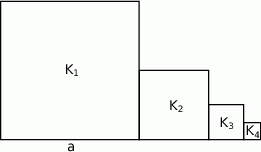
Wyznacz pole kwadratu 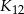 .
.
Różnica między polem koła opisanego na kwadracie a polem koła wpisanego w kwadrat jest równa 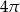 . Oblicz pole kwadratu.
. Oblicz pole kwadratu.
Oblicz pole kwadratu wiedząc, że różnica pól kół opisanego i wpisanego w ten kwadrat jest równa 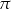 .
.
Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 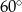 . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do
. Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 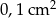 .
.
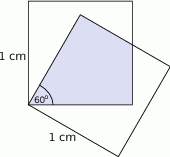
W kwadrat wpisano drugi kwadrat, którego wierzchołki leżą na bokach pierwszego i boki tworzą z bokami pierwszego kwadratu kąty o miarach 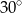 . Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
. Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
Dwa kwadraty 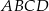 i
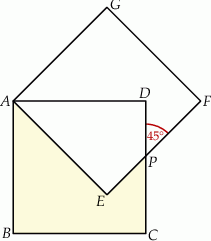
i 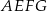 o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta
o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta 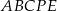 .
.
Dany jest kwadrat 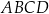 o boku długości
o boku długości  . Punkt
. Punkt 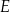 jest środkiem boku
jest środkiem boku 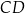 . Przekątna
. Przekątna 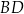 dzieli trójkąt
dzieli trójkąt 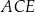 na dwie figury:
na dwie figury: 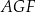 oraz
oraz 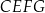 (zobacz rysunek).
(zobacz rysunek).
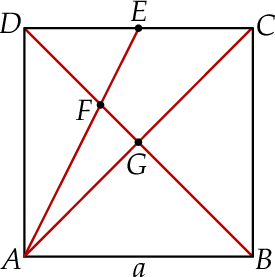
Oblicz pola figur 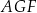 oraz
oraz 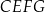 .
.
Wierzchołki kwadratu 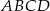 połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat
połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 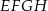 . Oblicz, jaki jest stosunek obwodów kwadratów
. Oblicz, jaki jest stosunek obwodów kwadratów 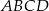 i
i  .
.
Niech 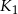 będzie kwadratem o boku długości
będzie kwadratem o boku długości  . Konstruujemy kolejno kwadraty
. Konstruujemy kolejno kwadraty 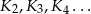 takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów
takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów 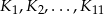 .
.
