Długości wszystkich krawędzi ostrosłupa czworokątnego prawidłowego są równe  . Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
. Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Przekroje
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 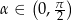 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 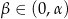 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe
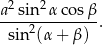
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego 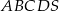 jest równa
jest równa  , a wysokość tego ostrosłupa ma długość
, a wysokość tego ostrosłupa ma długość 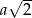 . Punkty
. Punkty 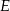 i
i 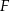 są środkami krawędzi bocznych odpowiednio
są środkami krawędzi bocznych odpowiednio 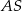 i
i 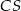 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 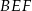 .
.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 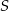 , a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę
, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę  . Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
. Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
Krawędź podstawy ostrosłupa prawidłowego czworokątnego 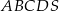 ma długość
ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 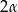 . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
. Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 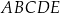 punkt
punkt 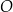 jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy
jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy 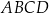 do sumy długości wszystkich krawędzi ostrosłupa jest równy 1:5. Przez przekątną
do sumy długości wszystkich krawędzi ostrosłupa jest równy 1:5. Przez przekątną 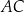 podstawy i środek
podstawy i środek 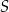 krawędzi bocznej
krawędzi bocznej 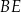 poprowadzono płaszczyznę. Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miarę kąta
poprowadzono płaszczyznę. Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miarę kąta 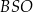 (w zaokrągleniu do
(w zaokrągleniu do 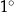 ).
).
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy 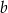 i kącie nachylenia krawędzi bocznej do krawędzi podstawy
i kącie nachylenia krawędzi bocznej do krawędzi podstawy  . Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem
. Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem 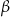 . Podaj konieczne założenia dotyczące kąta
. Podaj konieczne założenia dotyczące kąta  .
.
W ostrosłupie prawidłowym czworokątnym kąt ostry ściany bocznej przy wierzchołku ostrosłupa ma miarę  . Oblicz tangens kąta ostrego
. Oblicz tangens kąta ostrego 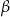 , jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy.
, jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy.
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
Przekrój ostrosłupa prawidłowego czworokątnego zawierającego przekątną podstawy oraz wierzchołek ostrosłupa jest trójkątem równobocznym o polu 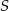 . Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
. Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
Ostrosłup prawidłowy czworokątny przecięto płaszczyzna przechodzącą przez krawędź podstawy i przecinającą przeciwległe krawędzie boczne w punktach jednakowo odległych od wierzchołka ostrosłupa. Przekrój ten jest trapezem o podstawach długości 12 i 8. Oblicz pole tego przekroju, jeżeli wysokość ostrosłupa ma długość 18.
Dany jest ostrosłup prawidłowy czworokątny 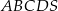 o podstawie
o podstawie 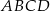 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze  takim, że
takim, że 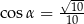 . Przez krawędź
. Przez krawędź 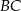 podstawy ostrosłupa poprowadzono płaszczyznę
podstawy ostrosłupa poprowadzono płaszczyznę 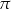 prostopadłą do ściany bocznej
prostopadłą do ściany bocznej 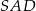 . Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę
. Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę 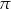 i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.
i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2,5 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.

