Stereometria/Geometria/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria

Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 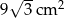√ -- 2 9 3 cm , a jego pole powierzchni bocznej jest równe 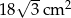√ -- 18 3 cm 2 . Oblicz objętość tego ostrosłupa.

Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.

Podstawą ostrosłupa 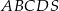ABCDS jest prostokąt o obwodzie 6. Krawędź 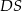jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi 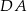. Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki 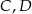C,D i środek krawędzi ?

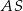Spośród tych graniastosłupów prawidłowych trójkątnych, których suma długości wszystkich krawędzi jest równa 18, wybierz graniastosłup o największej objętości. Oblicz tę maksymalną objętość.

Ukryj Podobne zadania

Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?

Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe 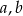a,b i . Krawędzie i 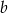są prostopadłe, a krawędź tworzy z każdą z nich kąt ostry . Oblicz objętość równoległościanu.

Podstawą ostrosłupa 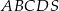ABCDS jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 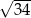√ --- 34 . Krawędź 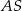jest wysokością ostrosłupa oraz 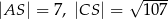√ ---- |AS | = 7, |CS | = 107 . Oblicz objętość tego ostrosłupa.

Dany jest stożek o polu powierzchni bocznej równym 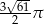3√-61 2 π , w którym tangens kąta nachylenia tworzącej do podstawy jest równy . Oblicz objętość tego stożka.

Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 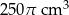250π cm 3 zużyć jak najmniej materiału na jej wykonanie.

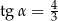Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze taki, że tg α = 43 .

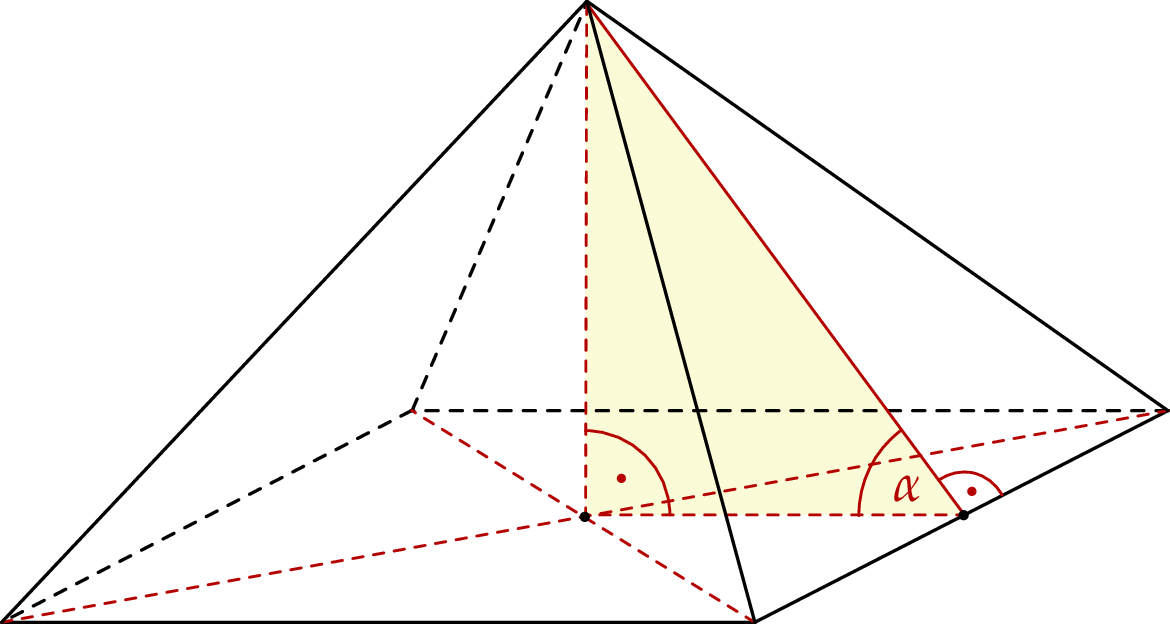
ZINFO-FIGURE

Oblicz wysokość ściany bocznej tego ostrosłupa.

Ukryj Podobne zadania

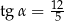Objętość ostrosłupa prawidłowego czworokątnego jest równa 400. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze taki, że tg α = 125- .

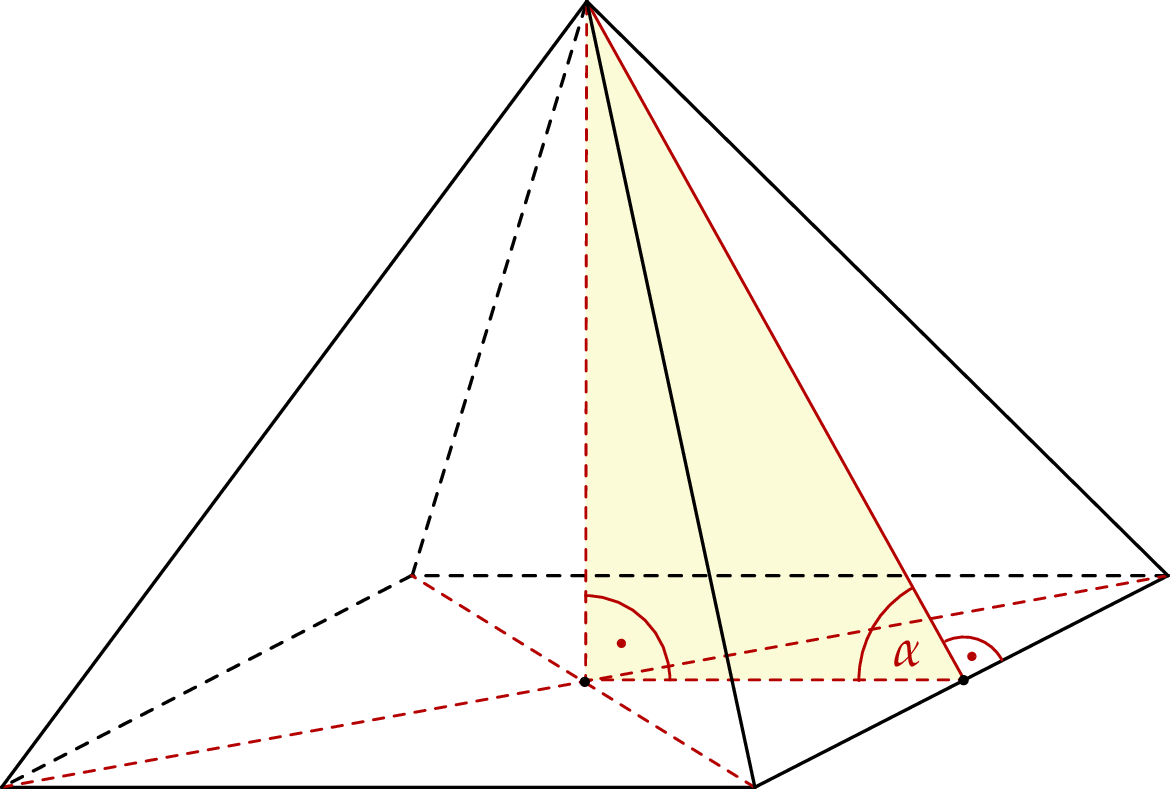
ZINFO-FIGURE

Oblicz wysokość ściany bocznej tego ostrosłupa.

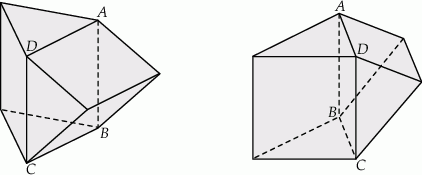
Na rysunkach przedstawiono tę samą bryłę widzianą z dwóch stron. Każda ze ścian tej bryły jest albo kwadratem, albo trójkątem równobocznym. Kwadratem jest też czworokąt ABCD (patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.

Ukryj Podobne zadania

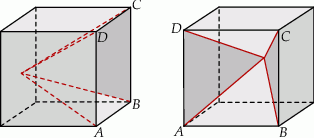
Z drewnianego sześcianu o krawędzi długości 6 cm wycięto ostrosłup prawidłowy czworokątny o wysokości równej krawędzi sześcianu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Jaką objętość ma ta bryła? Zapisz obliczenia.

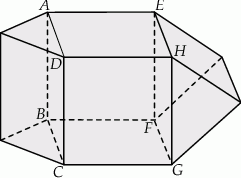
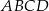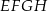Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty ABCD i EF GH . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.

W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.

Ukryj Podobne zadania

W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.

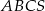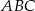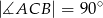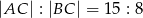Podstawą ostrosłupa trójkątnego ABCS jest trójkąt prostokątny ABC , w którym |∡ACB | = 9 0∘ i |AC | : |BC | = 15 : 8 (zobacz rysunek). Punkt 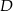jest środkiem okręgu opisanego na trójkącie 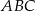ABC , a odcinek 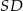jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany 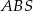ABS jest równe 17. Oblicz długość krawędzi 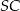ostrosłupa

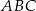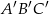Dany jest graniastosłup prawidłowy trójkątny o podstawach ABC i ′ ′ ′ A B C oraz krawędziach bocznych 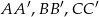AA ′,BB ′,CC ′ . Kąt nachylenia przekątnej ściany bocznej 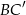BC ′ do płaszczyzny podstawy ma miarę . Promień okręgu wpisanego w podstawę graniastosłupa ma długość . Oblicz objętość tego graniastosłupa.

W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ostrosłupa ma miarę , zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa 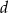. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Przekątna 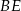ściany bocznej prostopadłościanu 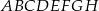ABCDEF GH tworzy z krawędzią podstawy 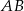kąt o mierze 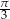π3- . Przekątne 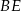i 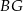ścian bocznych tworzą kąt, którego cosinus jest równy 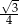√ - --3 4 , a krawędź 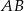podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie EBG .

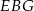Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.

W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 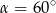α = 60∘ . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt .

Ukryj Podobne zadania

W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 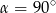α = 90∘ . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt .

Objętość graniastosłupa prawidłowego trójkątnego jest równa 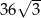√ -- 36 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.

Ukryj Podobne zadania

Objętość graniastosłupa prawidłowego trójkątnego jest równa 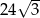√ -- 24 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.

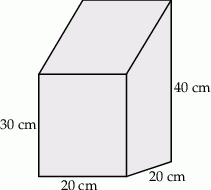
Spawacz ma wykonać z blachy konstrukcję, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary elementów są podane na rysunku. Oblicz pole powierzchni tej konstrukcji (wszystkich sześciu ścian). Wynik podaj z zaokrągleniem do 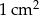1 cm 2 .

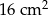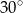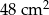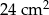Dany jest graniastosłup, którego podstawą jest równoległobok o polu 2 16 cm i kącie ostrym 30∘ . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 48 cm 2 i 24 cm 2 .

Strona 26 z 28