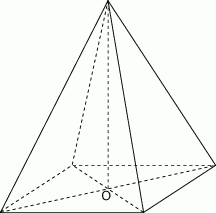
Dany jest ostrosłup prawidłowy czworokątny 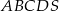 o podstawie
o podstawie 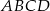 . W trójkącie równoramiennym
. W trójkącie równoramiennym 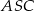 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 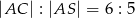 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
/Szkoła średnia/Geometria/Stereometria
Podstawą ostrosłupa 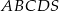 jest prostokąt
jest prostokąt 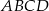 o bokach długości
o bokach długości 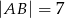 i
i 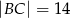 . Krawędź
. Krawędź 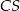 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 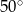 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Podstawą ostrosłupa jest romb. Wysokość ostrosłupa ma długość 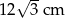 , a spodek
, a spodek 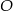 tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 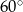 .
.
- Zaznacz na rysunku kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oraz poprowadź odcinek
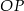 , którego długość jest równa odległości punktu
, którego długość jest równa odległości punktu 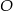 od ściany bocznej.
od ściany bocznej. - Oblicz odległość punktu
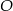 od ściany bocznej.
od ściany bocznej.
Trójkąt prostokątny o przyprostokątnych długości 12 i 7 obraca się wokół przeciwprostokątnej. Oblicz promień kuli wpisanej w otrzymaną bryłę.
Prostokąt 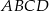 obracając się wokół boku
obracając się wokół boku 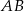 , zakreślił walec
, zakreślił walec 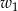 . Ten sam prostokąt obracając się wokół boku
. Ten sam prostokąt obracając się wokół boku 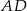 , zakreślił walec
, zakreślił walec 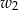 . Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt
. Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt 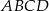 jest kwadratem.
jest kwadratem.
Wysokość podstawy graniastosłupa prawidłowego trójkątnego ma długość 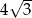 , zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy
, zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy 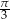 . Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
. Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
Oblicz stosunek objętości kuli wpisanej w czworościan foremny do objętości kuli opisanej na tym czworościanie.
W ostrosłup prawidłowy trójkątny wpisano kulę o promieniu  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 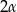 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Pole powierzchni bocznej stożka jest trzy razy większe od pola jego podstawy. Wysokość tego stożka jest równa 12. Oblicz objętość tego stożka.
Promień okręgu opisanego na podstawie graniastosłupa prawidłowego trójkątnego ma długość 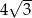 . Pole powierzchni bocznej jest równe 144.
. Pole powierzchni bocznej jest równe 144.
- Oblicz objętość tego graniastosłupa.
- Oblicz cosinus kąta między przekątną ściany bocznej i krawędzią podstawy graniastosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2,5 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
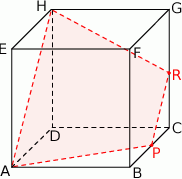
Dany jest sześcian  o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 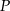 jest środkiem krawędzi
jest środkiem krawędzi 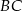 . Płaszczyzna
. Płaszczyzna 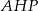 przecina krawędź
przecina krawędź 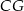 w punkcie
w punkcie 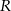 (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty
(zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty 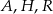 i
i 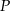 .
.
Suma długości wszystkich krawędzi ostrosłupa prawidłowego trójkątnego jest równa 96, a krawędź boczna tworzy z płaszczyzną podstawy kąt, którego cosinus jest równy 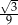 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa 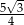 , a pole powierzchni bocznej tego ostrosłupa jest równe
, a pole powierzchni bocznej tego ostrosłupa jest równe 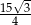 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W stożek o promieniu  i wysokości
i wysokości 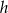 wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
Podstawą ostrosłupa jest kwadrat 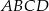 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 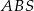 ,
, 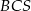 ,
, 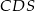 i
i 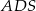 są odpowiednio równe: 740,
są odpowiednio równe: 740, 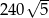 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 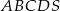 jest kwadrat
jest kwadrat 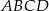 o boku długości 4. Odcinek
o boku długości 4. Odcinek 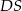 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 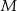 jest środkiem odcinka
jest środkiem odcinka 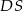 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 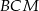 .
.
Do pojemnika w kształcie stożka wlano 1 litr wody, która wypełniła to naczynie do 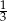 wysokości. Jaka jest całkowita pojemność tego naczynia?
wysokości. Jaka jest całkowita pojemność tego naczynia?
Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.

