Podstawą ostrosłupa 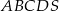 jest romb
jest romb 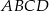 , w którym
, w którym 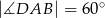 . Krawędź
. Krawędź 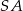 jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany
jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany 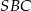 do płaszczyzny podstawy.
do płaszczyzny podstawy.
/Szkoła średnia/Geometria/Stereometria
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 100, a pole powierzchni ścian bocznych 320. Oblicz objętość ostrosłupa.
Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 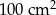 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 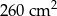 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne o krawędzi bocznej równej 3. Oblicz pole powierzchni całkowitej tego z tych ostrosłupów, dla którego pole przekroju płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy oraz wierzchołek ostrosłupa jest największe możliwe.
Odległość środka wysokości ostrosłupa prawidłowego trójkątnego od ściany bocznej jest równa 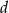 . Krawędź boczna tworzy z płaszczyzną podstawy kąt
. Krawędź boczna tworzy z płaszczyzną podstawy kąt  . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości 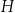 ostrosłupa oraz promienia
ostrosłupa oraz promienia 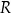 okręgu opisanego na podstawie tego ostrosłupa jest równa 6.
okręgu opisanego na podstawie tego ostrosłupa jest równa 6.
-
Wykaż, że objętość
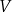 każdego z takich ostrosłupów w zależności od długości
każdego z takich ostrosłupów w zależności od długości 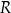 promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem
promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem 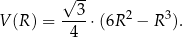
-
Wyznacz długość promienia okręgu opisanego na podstawie tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.
Czworościan foremny o krawędzi  rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości
rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości 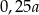 od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
Przekrój ostrosłupa prawidłowego trójkątnego 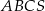 płaszczyzną przechodzącą przez wierzchołek
płaszczyzną przechodzącą przez wierzchołek 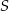 i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość
i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 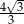 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 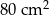 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 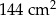 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
Udowodnij, że suma długości wysokości ścian bocznych ostrosłupa pięciokątnego jest nie większa niż suma długości jego krawędzi bocznych.
W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 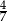 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 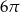 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi ścianami bocznymi ostrosłupa.
między sąsiednimi ścianami bocznymi ostrosłupa.
W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 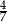 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 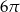 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi krawędziami bocznymi ostrosłupa.
między sąsiednimi krawędziami bocznymi ostrosłupa.
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 12 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 5. Jedna z krawędzi bocznych tego ostrosłupa ma długość 9 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 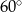 , a krawędź boczna ostrosłupa ma długość
, a krawędź boczna ostrosłupa ma długość 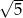 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny 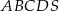 , którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 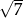 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
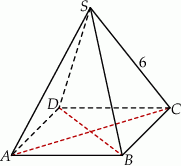
W ostrosłupie prawidłowym czworokątnym 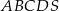 krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę
krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 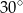 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 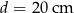 , wysokości
, wysokości 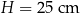 i tworzącej
i tworzącej 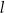 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 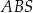 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 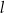 i środku
i środku 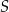 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 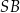 z odcinkiem
z odcinkiem 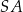 .
.

Oblicz miarę kąta 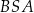 wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta
wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta 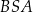 podaj w zaokrągleniu do jednego stopnia.
podaj w zaokrągleniu do jednego stopnia.
Częścią wspólną płaszczyzny 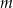 i kuli
i kuli 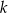 o środku
o środku 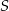 i promieniu
i promieniu 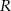 jest koło
jest koło  . Jaka musi być odległość płaszczyzny
. Jaka musi być odległość płaszczyzny 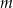 od środka kuli
od środka kuli 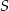 , aby stożek o podstawie
, aby stożek o podstawie  i wierzchołku
i wierzchołku 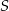 miał największą możliwą objętość? Oblicz tę maksymalną objętość.
miał największą możliwą objętość? Oblicz tę maksymalną objętość.
W ostrosłupie prawidłowym sześciokątnym dany jest kąt nachylenia ściany bocznej do płaszczyzny podstawy  . Oblicz stosunek pola podstawy do pola powierzchni bocznej ostrosłupa.
. Oblicz stosunek pola podstawy do pola powierzchni bocznej ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny 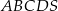 o podstawie
o podstawie 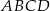 . Krawędź boczna tego ostrosłupa jest o
. Krawędź boczna tego ostrosłupa jest o 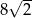 dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa 80, pole powierzchni całkowitej jest równe 256 i długości wszystkich krawędzi są nie mniejsze niż 4. Udowodnij, że liczba  może być długością krawędzi takiego prostopadłościanu wtedy i tylko wtedy, gdy
może być długością krawędzi takiego prostopadłościanu wtedy i tylko wtedy, gdy ![[ 28] c ∈ 4, 3](https://img.zadania.info/zad/1810762/HzadT1x.png) .
.
Punkty 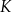 i
i 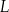 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 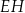 i
i 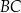 prostopadłościanu
prostopadłościanu 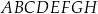 . Przez krawędź
. Przez krawędź 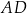 poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem
poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem 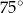 i płaszczyzna ta przecięła odcinek
i płaszczyzna ta przecięła odcinek 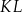 w punkcie
w punkcie 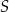 (zobacz rysunek).
(zobacz rysunek).
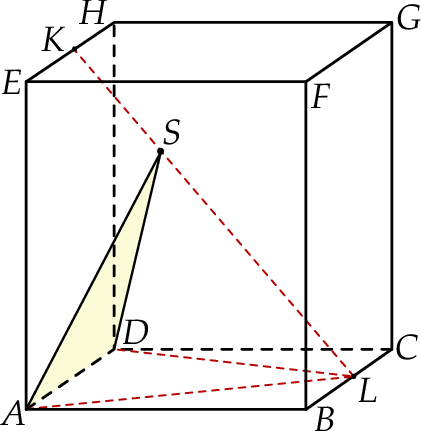
Oblicz pole trójkąta 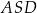 jeżeli
jeżeli 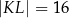 ,
, 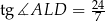 i
i 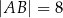 .
.
Podstawą ostrosłupa jest kwadrat o boku  . Dwie sąsiednie ściany boczne ostrosłupa są prostopadłe do płaszczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt
. Dwie sąsiednie ściany boczne ostrosłupa są prostopadłe do płaszczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt  . Oblicz pole powierzchni bocznej ostrosłupa.
. Oblicz pole powierzchni bocznej ostrosłupa.

