Stereometria/Geometria/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria

Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę 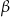. Wszystkie krawędzie boczne mają długość 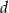i są nachylone do płaszczyzny podstawy pod kątem o mierze . Oblicz objętość tego ostrosłupa.

W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna 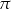, równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej 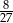-8 27 objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka 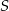kuli od płaszczyzny 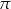, tj. długość najkrótszego spośród odcinków 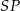, gdzie 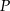jest punktem płaszczyzny .

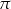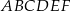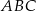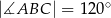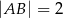Podstawą graniastosłupa prostego ABCDEF jest trójkąt ABC , w którym |∡ABC | = 120∘ oraz |AB | = 2 (zobacz rysunek). Trójkąt 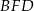BF D jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.

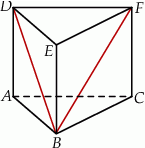
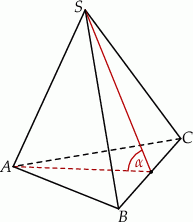
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 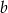, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę . Oblicz objętość tego ostrosłupa.

Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.

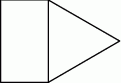
Pole narysowanego trójkąta jest równe 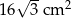√ -- 16 3 cm 2 , a pole prostokąta jest równe 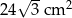√ -- 24 3 cm 2 . Oblicz objętość tego graniastosłupa.

Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 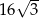√ -- 16 3 , a jego objętość 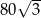√ -- 80 3 . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

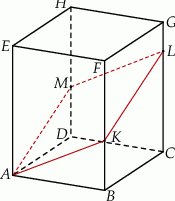
Podstawą graniastosłupa prostego 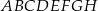ABCDEF GH jest romb o boku długości 5, polu 24 i kącie ostrym 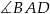∡BAD . Graniastosłup ten przecięto płaszczyzną 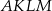AKLM w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym 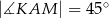|∡KAM | = 45 ∘ (zobacz rysunek). Oblicz pole tego przekroju.

Objętość ostrosłupa prawidłowego trójkątnego 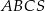ABCS (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę ABC tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.

Ukryj Podobne zadania

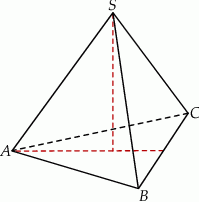
Objętość ostrosłupa prawidłowego trójkątnego ABCS (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie ABC tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.

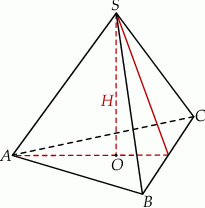
Objętość ostrosłupa prawidłowego trójkątnego 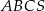ABCS (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę 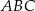ABC tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.

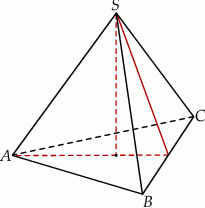
Objętość ostrosłupa prawidłowego trójkątnego 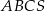ABCS (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 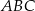ABC tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.

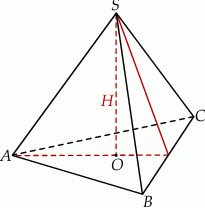
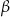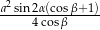Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym i przeciwprostokątnej długości . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe a2sin2α(cosβ+-1) 4cosβ .

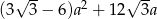Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy wyraża się wzorem √ -- √ -- (3 3 − 6)a2 + 12 3a . Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.

Trójkąt równoramienny o kącie 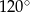∘ 120 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.

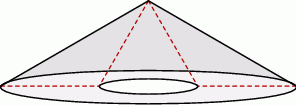
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.

Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).

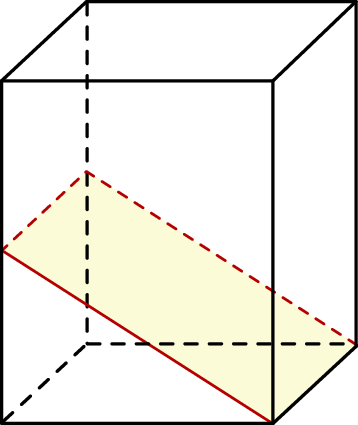
ZINFO-FIGURE

Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.

Przekrój osiowy stożka jest trójkątem równobocznym o polu 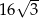√ -- 16 3 . Oblicz objętość i pole powierzchni całkowitej tego stożka.

Środki ścian sześcianu są wierzchołkami innej bryły – ośmiościanu foremnego (zobacz rysunek).

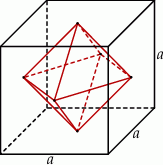
Oblicz objętość tego ośmiościanu jeżeli krawędź sześcianu ma długość .

Pole powierzchni bocznej stożka jest czterokrotnie większe od pola podstawy stożka. Oblicz wysokość stożka, wiedząc, że promień jego podstawy jest równy .

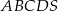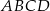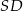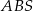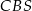Podstawą ostrosłupa ABCDS jest kwadrat ABCD . Krawędź boczna jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi ABS i CBS tego ostrosłupa.

Ukryj Podobne zadania

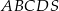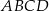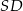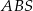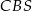Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości , a krawędź boczna jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi ABS i CBS tego ostrosłupa jest równy − 1 5 .

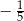Punkty 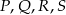P ,Q ,R ,S są środkami odpowiednio krawędzi 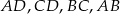AD ,CD ,BC ,AB czworościanu 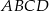ABCD . Wykaż, że punkty 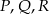P ,Q,R i 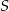są wierzchołkami równoległoboku.

Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości 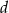tworzy z wysokością kąt o mierze .

Wyprowadź wzór na objętość walca.
Oblicz tę objętość dla 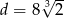i .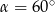

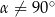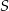W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α ⁄= 90∘ . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę jest równe . Oblicz objętość graniastosłupa.

Strona 2 z 28