Ze zbioru wszystkich liczb naturalnych ośmiocyfrowych, w których zapisie dziesiętnym występują tylko cyfry ze zbioru 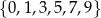 , losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
, losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
/Szkoła średnia/Prawdopodobieństwo
Spośród liczb naturalnych ośmiocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby o sumie cyfr równej 4, jeżeli wiadomo, że żadna cyfra wylosowanej liczby nie jest równa 2, 3, 6 ani 8.
Na diagramie składającym się z 9 kwadratowych pól w układzie 3x3 zaznaczono w losowo wybranych polach kółko i krzyżyk. Jakie jest prawdopodobieństwo tego, że oba znaki znalazły się na sąsiednich polach tzn. stykających się jednym bokiem.
Ze zbioru punktów o współrzędnych 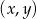 , gdzie
, gdzie 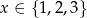 zaś
zaś 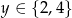 wybrano losowo dwa różne punkty. Oblicz prawdopodobieństwa zdarzeń:
wybrano losowo dwa różne punkty. Oblicz prawdopodobieństwa zdarzeń:
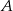 – wylosowane punkty należą do prostej o równaniu
– wylosowane punkty należą do prostej o równaniu 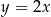 ;
; 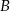 – wylosowane punkty są końcami odcinka równoległego do osi
– wylosowane punkty są końcami odcinka równoległego do osi 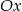 .
.
Po przypadkowo wybranych równoległych do siebie torach czterotorowej linii kolejowej jadą naprzeciw siebie 2 drezyny. Oblicz prawdopodobieństwo ich zderzenia.
Na stu mężczyzn ośmiu, zaś na tysiąc kobiet pięć ma zaburzenie rozpoznawania barw. Z grupy, w której stosunek liczby mężczyzn do liczby kobiet wynosi 7:11 wybrano losowo jedną osobę. Jakie jest prawdopodobieństwo, że wylosowana osoba prawidłowo rozpoznaje kolory?
W pierwszej loterii jest 
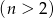 losów, spośród których jeden wygrywa, a w drugiej jest
losów, spośród których jeden wygrywa, a w drugiej jest 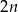 losów, spośród których dwa wygrywają. Gracz chce kupić dwa losy w jednej z tych loterii. W której z nich ma większą szansę otrzymania co najmniej jednego losu wygrywającego?
losów, spośród których dwa wygrywają. Gracz chce kupić dwa losy w jednej z tych loterii. W której z nich ma większą szansę otrzymania co najmniej jednego losu wygrywającego?
Przedstawiono informacje dotyczące znajomości języka angielskiego oraz języka niemieckiego w pewnej 200 osobowej grupie studentów:
25% studentów zna język angielski i język niemiecki,
50% studentów zna język niemiecki,
60% zna język angielski.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany z tej grupy student
- zna język angielski i nie zna języka niemieckiego,
- nie zna języka angielskiego i nie zna języka niemieckiego.
Spośród cyfr 1, 2, 3, 4, 5, 6 losujemy kolejno dwa razy po jednej cyfrze ze zwracaniem. Tworzymy liczbę dwucyfrową w ten sposób, że pierwsza z wylosowanych cyfr jest cyfrą dziesiątek, a druga cyfrą jedności tej liczby. Oblicz prawdopodobieństwo utworzenia liczby większej od 52.
Spośród liczb 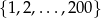 wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa
wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa 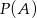 i
i 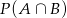 , gdzie
, gdzie 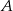 i
i 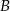 są następującymi zdarzeniami:
są następującymi zdarzeniami: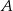 – druga z wylosowanych liczb jest mniejsza od 2;
– druga z wylosowanych liczb jest mniejsza od 2;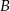 – różnica wylosowanych liczb jest podzielna przez 3.
– różnica wylosowanych liczb jest podzielna przez 3.
Ze zbioru liczb 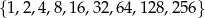 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 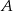 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 2 kule czarne. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo dokładamy do urny drugiej jeszcze dwie kule tego samego koloru, co wylosowana kula. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą białe.
W pierwszej urnie umieszczono 5 kul białych i 4 kule czarne, a w drugiej urnie 6 kul białych i 7 kul czarnych. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo wyjmujemy z drugiej urny jeszcze dwie kule koloru innego, niż kolor wylosowanej kuli. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą czarne.
W pierwszej urnie są 4 kule zielone i 5 czerwonych, w drugiej urnie 3 zielone i 6 czerwonych. Z pierwszej urny losujemy jedną kulę i przekładamy ją do drugiej urny. Następnie do drugiej urny dokładamy 2 kule tego samego koloru co wylosowana kula. Losujemy dwie kule z drugiej urny. Oblicz prawdopodobieństwo, że obie będą zielone.
Liczbę naturalną nazywamy palindromiczną, jeżeli nie zmienia się po zapisaniu jej cyfr w odwrotnej kolejności. Liczbami palindromicznymi są np. liczby 5, 33, 1123211. Liczby 10, 3230 nie są palindromiczne.
- Oblicz prawdopodobieństwo, że losowo wybrana liczba siedmiocyfrowa jest liczbą palindromiczną.
- Oblicz prawdopodobieństwo, że suma dwóch losowo wybranych liczb dwucyfrowych jest nieparzystą dwucyfrową liczbą palindromiczną.
Egzamin składa się z 15 zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej 11 zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny. Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 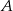 polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
Siedmiokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników jest 5 czwórek. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy czwórkę?
Sześciokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników są dokładnie trzy dwójki. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy piątkę?
Ośmiokrotnie rzucamy sześcienną kostką do gry. Wśród otrzymanych wyników jest dokładnie 5 piątek. Jakie jest prawdopodobieństwo, że w ostatnim rzucie otrzymaliśmy piątkę?
Wykaż, że jeżeli 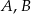 są podzbiorami
są podzbiorami 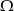 oraz
oraz 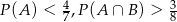 , to
, to 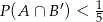 .
.
Wykaż, że jeżeli 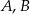 są podzbiorami
są podzbiorami 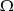 oraz
oraz 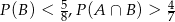 , to
, to 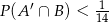 (
(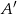 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 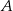 ).
).
Wykaż, że jeżeli prawdopodobieństwa zdarzeń 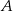 i
i 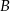 spełniają warunki:
spełniają warunki: 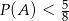 i
i 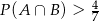 , to
, to
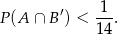
Rzucamy sześcienną kostką do gry tak długo, aż otrzymamy co najmniej dwie nieparzyste liczby oczek, albo 10 parzystych liczb oczek. Oblicz prawdopodobieństwo, że w przeprowadzonym doświadczeniu otrzymaliśmy liczbę oczek równą 5, przy założeniu, że otrzymaliśmy tylko jedną nieparzystą liczbę oczek.
Z dworca prowadzą dwa wyjścia: wyjście 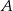 na przystanek autobusowy oraz
na przystanek autobusowy oraz 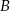 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 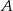 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 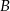 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą wyjście
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą wyjście 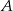 .
.
Z dworca prowadzą dwa wyjścia: wyjście 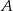 na przystanek autobusowy oraz
na przystanek autobusowy oraz 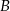 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 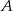 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 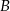 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że tylko dwaj z nich wybiorą to samo wyjście.
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że tylko dwaj z nich wybiorą to samo wyjście.
Z dworca prowadzą dwa wyjścia: wyjście 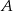 na przystanek autobusowy oraz
na przystanek autobusowy oraz 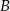 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 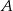 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 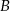 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą to samo wyjście.
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą to samo wyjście.
Z dworca prowadzą dwa wyjścia: wyjście 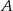 na przystanek autobusowy oraz
na przystanek autobusowy oraz 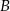 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 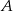 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 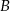 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że jeden wybierze wyjście
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że jeden wybierze wyjście 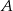 , a pozostali dwaj, wyjście
, a pozostali dwaj, wyjście 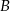 .
.
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy kolejno trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 304.
W dwunastu rzutach monetą cztery razy wypadł orzeł. Oblicz prawdopodobieństwo, że orzeł wypadł w piątym rzucie tej serii rzutów.

