W okrąg o równaniu 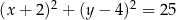 wpisano trójkąt
wpisano trójkąt 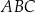 , którego pole jest równe 20. Bok
, którego pole jest równe 20. Bok 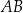 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 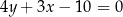 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 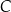 przecina bok
przecina bok 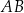 w punkcie
w punkcie 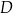 , którego obie współrzędne są dodatnie. Oblicz współrzędne punktu
, którego obie współrzędne są dodatnie. Oblicz współrzędne punktu 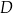 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Różne
Wierzchołek 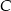 trójkąta
trójkąta 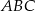 leży na okręgu o równaniu
leży na okręgu o równaniu 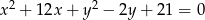 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 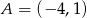 i
i 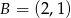 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
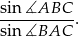
Boki trójkąta 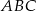 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 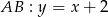 ,
, 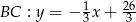 i
i 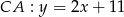 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 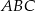 .
.
W trójkącie 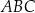 , w którym
, w którym 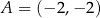 oraz
oraz 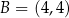 , kąt przy wierzchołku
, kąt przy wierzchołku 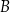 jest rozwarty. Bok
jest rozwarty. Bok 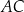 zawiera się w prostej
zawiera się w prostej 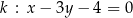 . Środek okręgu opisanego na trójkącie
. Środek okręgu opisanego na trójkącie 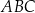 znajduje się w odległości
znajduje się w odległości 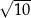 od boku
od boku 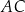 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Okrąg wpisany w trójkąt 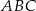 ma równanie
ma równanie 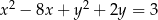 . Oblicz
. Oblicz 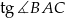 jeżeli
jeżeli 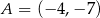 .
.
W układzie współrzędnych są dane punkty 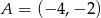 ,
, 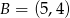 .
.
- Oblicz odległość punktu
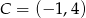 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 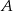 i
i 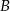 .
. - Uzasadnij, że jeśli
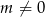 , to punkty
, to punkty 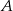 ,
, 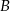 oraz punkt
oraz punkt 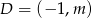 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Dane są dwa nieskończone ciągi 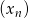 i
i 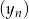 takie, że dla każdego
takie, że dla każdego 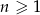 , punkt o współrzędnych
, punkt o współrzędnych 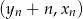 jest środkiem ciężkości trójkąta o wierzchołkach
jest środkiem ciężkości trójkąta o wierzchołkach 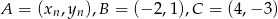 . Wyznacz wzory ciągów
. Wyznacz wzory ciągów 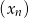 i
i 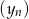 .
.
Proste 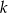 i
i 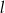 przecinają się w punkcie
przecinają się w punkcie 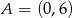 . Prosta
. Prosta 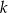 przecina ujemną półoś
przecina ujemną półoś 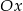 w punkcie
w punkcie 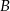 i tworzy z osiami układu trójkąt o polu 6, a prosta
i tworzy z osiami układu trójkąt o polu 6, a prosta 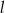 przecina dodatnią półoś
przecina dodatnią półoś 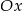 w punkcie
w punkcie 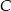 i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta
i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta 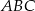 opuszczonej z wierzchołka
opuszczonej z wierzchołka 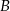 .
.
Punkt 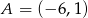 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 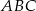 , a punkt
, a punkt 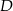 jest środkiem odcinka
jest środkiem odcinka 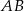 . Równania prostych
. Równania prostych 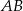 ,
, 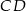 oraz symetralnej boku
oraz symetralnej boku 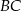 to odpowiednio
to odpowiednio 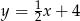 ,
, 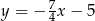 i
i 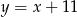 . Napisz równanie prostej zawierającej wysokość trójkąta
. Napisz równanie prostej zawierającej wysokość trójkąta 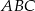 opuszczoną z wierzchołka
opuszczoną z wierzchołka 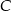 .
.
Punkty 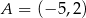 i
i 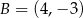 są wierzchołkami trójkąta
są wierzchołkami trójkąta 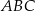 , a wysokości opuszczone z wierzchołków
, a wysokości opuszczone z wierzchołków 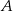 i
i 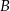 tego trójkąta zawierają się odpowiednio w prostych o równaniach
tego trójkąta zawierają się odpowiednio w prostych o równaniach 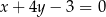 oraz
oraz 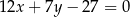 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 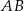 .
.
Punkty 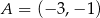 i
i 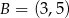 są wierzchołkami trójkąta
są wierzchołkami trójkąta 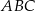 , a jego wysokości przecinają się w punkcie
, a jego wysokości przecinają się w punkcie 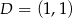 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 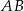 .
.
Prosta 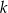 tworzy z dodatnią półosią
tworzy z dodatnią półosią 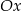 kąt o mierze
kąt o mierze 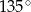 i przechodzi przez punkt
i przechodzi przez punkt 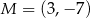 . Prosta
. Prosta 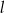 jest prostopadła do prostej
jest prostopadła do prostej 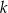 i przecina oś
i przecina oś 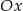 w punkcie o odciętej
w punkcie o odciętej 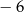 . Oblicz obwód trójkąta utworzonego przez proste
. Oblicz obwód trójkąta utworzonego przez proste 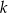 ,
, 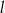 i oś
i oś 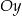 .
.
Punkty 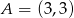 i
i 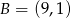 są wierzchołkami trójkąta
są wierzchołkami trójkąta 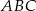 , a punkt
, a punkt 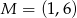 jest środkiem boku
jest środkiem boku 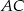 . Oblicz współrzędne punktu przecięcia prostej
. Oblicz współrzędne punktu przecięcia prostej 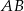 z wysokością tego trójkąta, poprowadzoną z wierzchołka
z wysokością tego trójkąta, poprowadzoną z wierzchołka 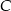 .
.
W kartezjańskim układzie współrzędnych  punkt
punkt 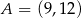 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 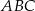 . Prosta
. Prosta 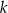 o równaniu
o równaniu 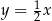 zawiera dwusieczną kąta
zawiera dwusieczną kąta 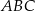 tego trójkąta. Okrąg
tego trójkąta. Okrąg 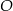 o równaniu
o równaniu 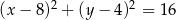 jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki
jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki 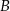 i
i 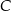 tego trójkąta z okręgiem
tego trójkąta z okręgiem 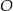 .
.
Boki 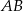 i
i 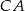 trójkąta
trójkąta 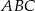 są zawarte w prostych
są zawarte w prostych 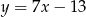 i
i 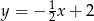 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 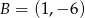 i
i 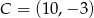 . Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok
. Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok 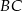 .
.

