W trójkącie 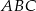 , gdzie
, gdzie 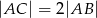 dane są
dane są 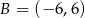 i
i 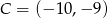 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 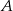 , jeżeli leży on na prostej
, jeżeli leży on na prostej 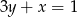 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków
Pole trójkąta 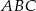 o danych wierzchołkach
o danych wierzchołkach 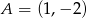 oraz
oraz 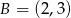 jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu
jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu 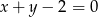 .
.
Znajdź taki punkt 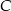 , leżący na prostej
, leżący na prostej 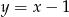 , aby pole trójkąta
, aby pole trójkąta 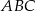 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 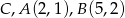 było równe 5.
było równe 5.
Dane są punkty 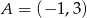 i
i 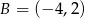 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 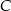 na prostej
na prostej 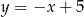 tak, aby pole trójkąta
tak, aby pole trójkąta 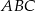 było równe 7.
było równe 7.
Punkty 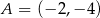 i
i 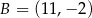 są wierzchołkami trójkąta
są wierzchołkami trójkąta 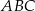 . Wierzchołek
. Wierzchołek 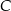 tego trójkąta leży na prostej
tego trójkąta leży na prostej 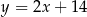 , a dwusieczna kąta
, a dwusieczna kąta 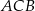 przecina bok
przecina bok 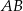 w punkcie
w punkcie 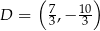 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 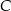 trójkąta
trójkąta 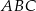 .
.
Okrąg wpisany w trójkąt 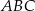 jest opisany równaniem
jest opisany równaniem
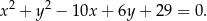
Punkty styczności tego okręgu z bokami 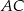 i
i 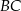 trójkąta
trójkąta 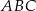 leżą na prostej o równaniu:
leżą na prostej o równaniu: 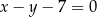 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 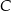 trójkąta
trójkąta 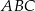 .
.
W trójkącie 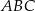 o polu 20 dane sa współrzędne dwóch wierzchołków:
o polu 20 dane sa współrzędne dwóch wierzchołków:  ,
, 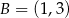 oraz środek
oraz środek 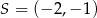 okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka
okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka 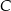 .
.
Znając współrzędne wierzchołków trójkąta 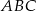 ,
, 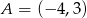 ,
, 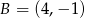 oraz punkt przecięcia się jego wysokości
oraz punkt przecięcia się jego wysokości 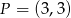 wyznacz współrzędne wierzchołka
wyznacz współrzędne wierzchołka 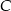 .
.
Punkty 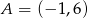 i
i 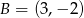 są wierzchołkami trójkąta
są wierzchołkami trójkąta 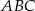 . Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne
. Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne 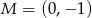 oblicz współrzędne wierzchołka
oblicz współrzędne wierzchołka 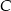 .
.
Wyznacz współrzędne wierzchołków trójkąta, którego boki zawarte są w prostych o równaniach 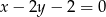 ,
, 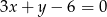 ,
, 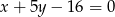 .
.
Punkty 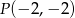 ,
, 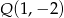 i
i 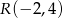 są środkami boków
są środkami boków 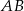 ,
, 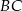 i
i 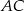 trójkąta
trójkąta 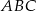 . Oblicz:
. Oblicz:
- Współrzędne wierzchołków trójkąta
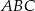 .
. - Obwód trójkąta
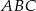 .
.
Odległość każdego z wierzchołków 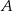 i
i 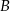 trójkąta
trójkąta 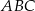 od punktu
od punktu 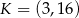 jest równa
jest równa 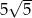 , a odległość tych wierzchołków od punktu
, a odległość tych wierzchołków od punktu 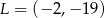 jest równa 25. Okrąg opisany na trójkącie
jest równa 25. Okrąg opisany na trójkącie 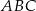 jest styczny do prostej
jest styczny do prostej 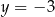 w punkcie
w punkcie 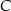 . Punkt
. Punkt 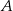 znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta
znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta 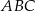 .
.
Wierzchołek 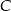 trójkąta ostrokątnego
trójkąta ostrokątnego 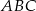 ma współrzędne
ma współrzędne 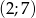 . Prosta o równaniu
. Prosta o równaniu 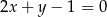 jest symetralną wysokości
jest symetralną wysokości 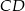 , a prosta o równaniu
, a prosta o równaniu 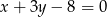 zawiera środkową trójkąta poprowadzoną z wierzchołka
zawiera środkową trójkąta poprowadzoną z wierzchołka 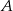 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 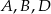 .
.
Dane są dwa wierzchołki trójkąta 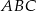 :
: 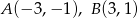 . Punkt
. Punkt 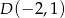 należy do boku
należy do boku 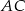 , a odcinek
, a odcinek 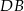 jest środkową w trójkącie
jest środkową w trójkącie 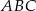 . Oblicz:
. Oblicz:
- współrzędne wierzchołka
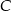 ;
; - pole trójkąta
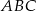 .
.
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 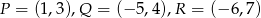 .
.
W kartezjańskim układzie współrzędnych 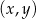 punkt
punkt 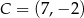 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 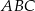 . Prosta
. Prosta 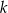 o równaniu
o równaniu 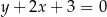 zawiera dwusieczną kąta
zawiera dwusieczną kąta 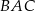 tego trójkąta. Okrąg
tego trójkąta. Okrąg 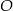 o równaniu
o równaniu 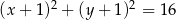 jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków
jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków 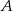 i
i 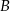 trójkąta
trójkąta 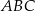 .
.

