W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy trójkątny
Dany jest graniastosłup prawidłowy trójkątny 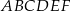 o podstawach
o podstawach 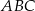 i
i 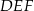 i krawędziach bocznych
i krawędziach bocznych 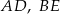 i
i 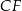 , które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta
, które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta 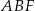 stanowi
stanowi 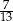 pola ściany bocznej
pola ściany bocznej 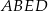 .
.
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe 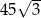 . Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
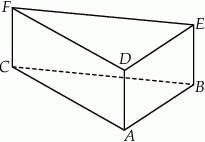
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Objętość tego graniastosłupa jest równa 324. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz pole powierzchni całkowitej tego graniastosłupa.
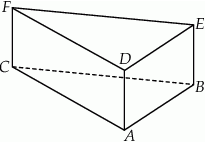
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 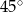 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 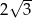 .
.
W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z płaszczyzną podstawy kąt o mierze równej 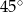 . Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa
. Oblicz pole powierzchni bocznej tego graniastosłupa, wiedząc, że jego objętość jest równa 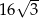 .
.
Długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa  . Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka
. Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka 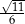 . Wyznacz pole powierzchni całkowitej tego graniastosłupa.
. Wyznacz pole powierzchni całkowitej tego graniastosłupa.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 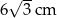 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 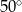 . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
. Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
Promień okręgu opisanego na podstawie graniastosłupa prawidłowego trójkątnego ma długość 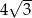 . Pole powierzchni bocznej jest równe 144.
. Pole powierzchni bocznej jest równe 144.
- Oblicz objętość tego graniastosłupa.
- Oblicz cosinus kąta między przekątną ściany bocznej i krawędzią podstawy graniastosłupa.
Dany jest graniastosłup prawidłowy trójkątny o podstawach 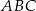 i
i 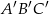 oraz krawędziach bocznych
oraz krawędziach bocznych 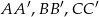 . Kąt nachylenia przekątnej ściany bocznej
. Kąt nachylenia przekątnej ściany bocznej 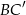 do płaszczyzny podstawy ma miarę
do płaszczyzny podstawy ma miarę  . Promień okręgu wpisanego w podstawę graniastosłupa ma długość
. Promień okręgu wpisanego w podstawę graniastosłupa ma długość  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 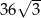 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 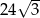 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy  i wysokości
i wysokości 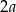 . Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 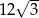 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 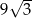 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę 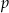 wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna 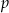 z płaszczyzną podstawy graniastosłupa tworzy kąt ostry
z płaszczyzną podstawy graniastosłupa tworzy kąt ostry  taki, że
taki, że 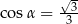 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę 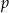 jest równe
jest równe 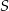 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.

