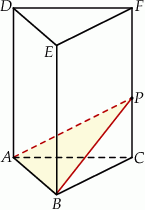
Przez punkt 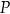 krawędzi bocznej
krawędzi bocznej 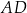 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 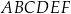 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
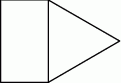
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 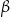 (zobacz rysunek).
(zobacz rysunek).
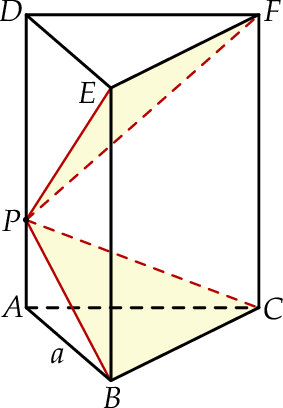
Udowodnij, że objętość ostrosłupa 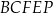 jest równa
jest równa
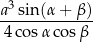

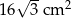 , a pole prostokąta jest równe
, a pole prostokąta jest równe 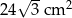 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna  z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze
z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze 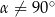 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę  jest równe
jest równe 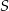 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.  . Oblicz długość krawędzi podstawy tego graniastosłupa.
. Oblicz długość krawędzi podstawy tego graniastosłupa. 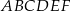 ma długość 4 (zobacz rysunek).
ma długość 4 (zobacz rysunek). 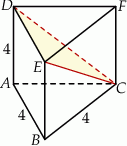
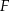 tego graniastosłupa od płaszczyzny
tego graniastosłupa od płaszczyzny 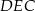 .
. 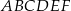 . Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
. Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek). 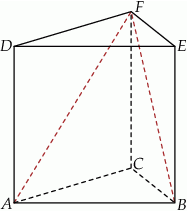
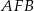 .
. 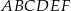 o podstawach
o podstawach 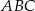 i
i 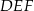 i krawędziach bocznych
i krawędziach bocznych 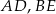 i
i 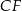 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 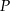 jest środkiem krawędzi
jest środkiem krawędzi 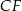 . Długość krawędzi podstawy
. Długość krawędzi podstawy 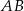 jest równa 12, a pole trójkąta
jest równa 12, a pole trójkąta 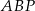 jest równe
jest równe 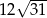 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 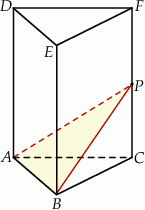
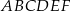 jest równa 6 (zobacz rysunek). Punkt
jest równa 6 (zobacz rysunek). Punkt 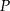 dzieli krawędź boczną
dzieli krawędź boczną 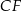 w stosunku
w stosunku 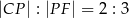 . Pole trójkąta
. Pole trójkąta 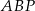 jest równe
jest równe 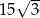 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 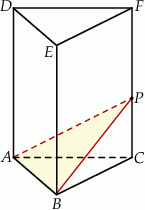
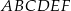 o podstawach
o podstawach 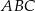 i
i 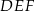 , w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy
, w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy 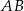 jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy
jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy 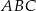 tego graniastosłupa pod takim kątem
tego graniastosłupa pod takim kątem  , że
, że 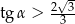 .
.  do dolnej podstawy. Pole otrzymanego przekroju wynosi
do dolnej podstawy. Pole otrzymanego przekroju wynosi 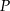 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. 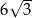 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 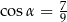 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa. 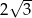 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 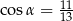 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa. 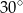 .
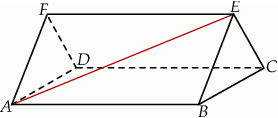
. 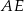 , ściany
, ściany 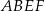 jest nachylona do ściany
jest nachylona do ściany 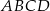 pod kątem ostrym
pod kątem ostrym  takim, że
takim, że 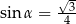 .
. 
 .
. 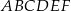 o podstawach
o podstawach 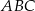 i
i 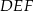 i krawędziach bocznych
i krawędziach bocznych 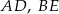 i
i 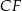 . Oblicz pole trójkąta
. Oblicz pole trójkąta 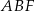 wiedząc, że
wiedząc, że 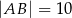 i
i 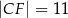 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 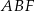 .
. 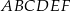 o podstawach
o podstawach 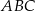 i
i 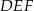 i krawędziach bocznych
i krawędziach bocznych 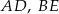 i
i 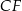 . Oblicz pole trójkąta
. Oblicz pole trójkąta 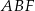 wiedząc, że
wiedząc, że 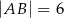 i
i 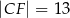 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 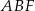 .
. 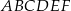 o podstawach
o podstawach 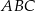 i
i 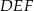 i krawędziach bocznych
i krawędziach bocznych 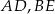 i
i 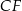 (zobacz rysunek). Długość krawędzi podstawy
(zobacz rysunek). Długość krawędzi podstawy 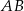 jest równa 8, a pole trójkąta
jest równa 8, a pole trójkąta 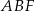 jest równe 52. Oblicz objętość tego graniastosłupa.
jest równe 52. Oblicz objętość tego graniastosłupa. 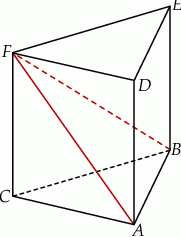
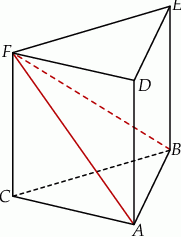
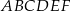 o podstawach
o podstawach 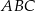 i
i 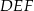 i krawędziach bocznych
i krawędziach bocznych 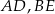 i
i 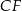 (zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta
(zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 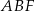 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 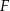 i płaszczyzną podstawy
i płaszczyzną podstawy 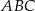 tego graniastosłupa jest równy
tego graniastosłupa jest równy 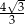 . Oblicz pole trójkąta
. Oblicz pole trójkąta 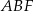 .
. 
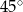 do dolnej podstawy. Pole otrzymanego przekroju wynosi
do dolnej podstawy. Pole otrzymanego przekroju wynosi 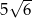 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 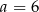 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 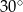 . Oblicz
. Oblicz 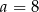 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 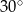 . Oblicz
. Oblicz 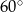 oblicz pole otrzymanego przekroju.
oblicz pole otrzymanego przekroju. 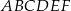 o podstawach
o podstawach 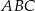 i
i 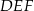 i krawędziach bocznych
i krawędziach bocznych 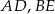 i
i 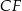 (zobacz rysunek). Przez krawędź
(zobacz rysunek). Przez krawędź 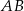 poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem
poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem 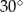 . Płaszczyzna ta przecina krawędź
. Płaszczyzna ta przecina krawędź 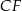 w punkcie
w punkcie 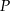 . Oblicz pole trójkąta
. Oblicz pole trójkąta 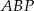 jeżeli objętość ostrosłupa
jeżeli objętość ostrosłupa 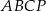 jest równa
jest równa 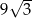 .
.