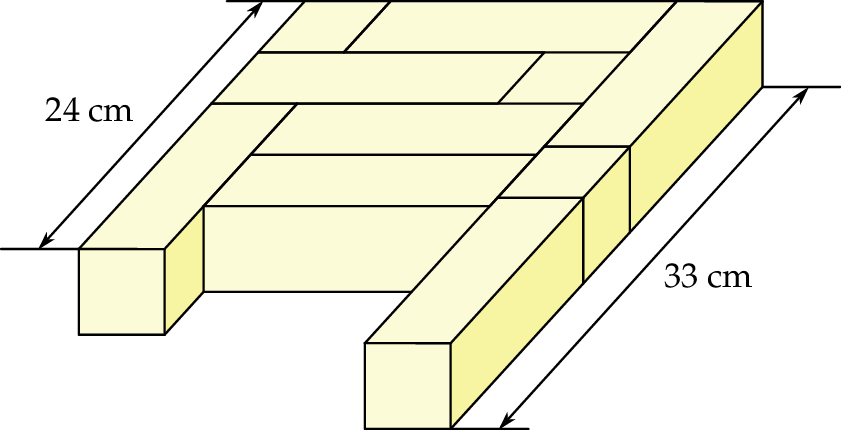
Karol ułożył figurę przedstawioną na rysunku. Figura została zbudowana z dwóch rodzajów klocków: sześciennych i prostopadłościennych. Wszystkie klocki tego samego rodzaju mają takie same wymiary.
Oblicz objętość bryły zbudowanej z tych klocków.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Karol ułożył figurę przedstawioną na rysunku. Figura została zbudowana z dwóch rodzajów klocków: sześciennych i prostopadłościennych. Wszystkie klocki tego samego rodzaju mają takie same wymiary.

Oblicz objętość bryły zbudowanej z tych klocków.
Objętość prostopadłościanu jest równa 405. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 3 : 5. Oblicz pole powierzchni całkowitej prostopadłościanu.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest kwadratem o boku 5 cm, a druga – prostokątem o bokach 3 cm i 5 cm.
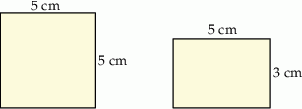
Oblicz sumę długości wszystkich krawędzi prostopadłościanu o takich wymiarach.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest prostokątem o bokach 6 cm i 9 cm, a druga – prostokątem o bokach 9 cm i 12 cm.
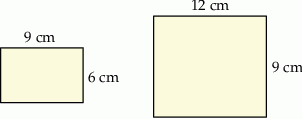
Oblicz pole powierzchni całkowitej prostopadłościanu o takich wymiarach.
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 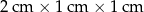 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
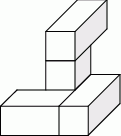
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 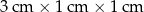 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
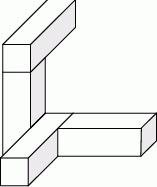
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
Powierzchnia kartonu ma kształt prostokąta o wymiarach 8 cm i 15 cm. W czterech rogach tego kartonu wycięto kwadraty o boku 2,5 cm. Z pozostałej części złożono pudełko.

Oblicz objętość tego pudełka.
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 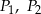 i
i 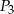 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 2 : 3. Oblicz długość przekątnej tego prostopadłościanu.
Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku.
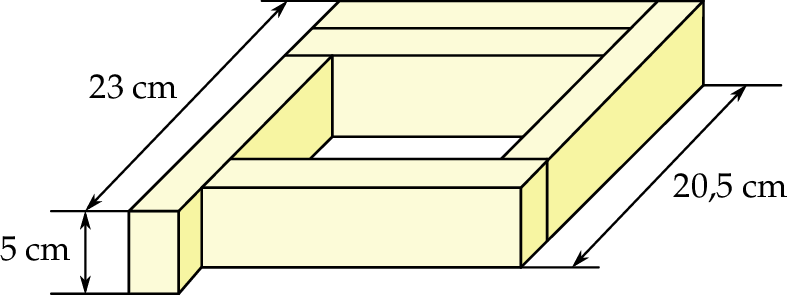
Oblicz objętość jednego klocka.
Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku.
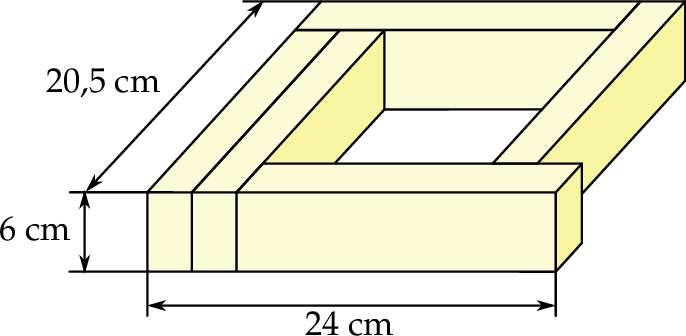
Oblicz objętość jednego klocka.
Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 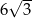 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
Oblicz pole powierzchni całkowitej i objętość prostopadłościanu 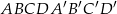 , w którym krawędź
, w którym krawędź 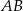 ma długość 10 cm i tworzy z przekątną
ma długość 10 cm i tworzy z przekątną 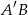 ściany bocznej kąt
ściany bocznej kąt 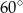 , a krawędź
, a krawędź 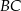 jest o cztery centymetry krótsza od krawędzi
jest o cztery centymetry krótsza od krawędzi 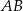 .
.
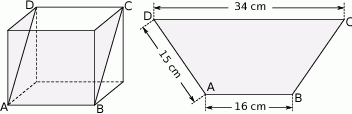
Powierzchnię boczną pudełka w kształcie graniastosłupa czworokątnego rozcięto wzdłuż przekątnych dwóch przeciwległych ścian bocznych i otrzymano dwa przystające trapezy. Podstawy otrzymanych trapezów mają długości 16 cm i 34 cm, a ich ramiona mają długość 15 cm. Oblicz objętość tego pudełka. Zapisz obliczenia.