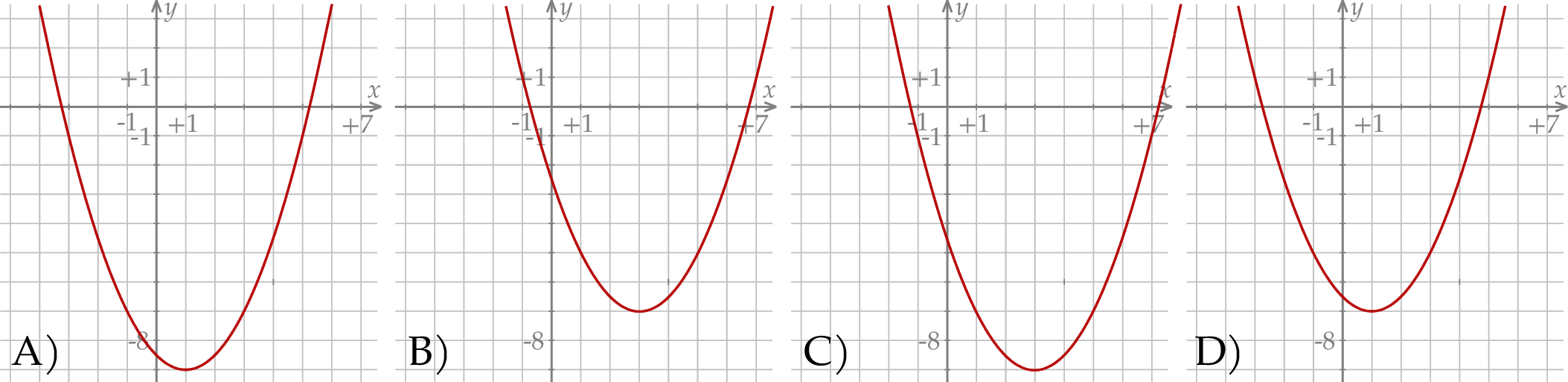
Wykresem funkcji kwadratowej 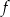 określonej wzorem
określonej wzorem 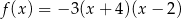 jest parabola o wierzchołku
jest parabola o wierzchołku 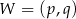 . Współrzędne wierzchołka
. Współrzędne wierzchołka 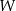 spełniają warunki
spełniają warunki
A) 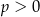 i
i 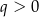 B)
B) 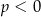 i
i 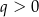 C)
C) 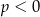 i
i 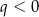 D)
D) 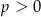 i
i 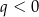
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola
Wykresem funkcji kwadratowej 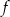 określonej wzorem
określonej wzorem 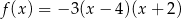 jest parabola o wierzchołku
jest parabola o wierzchołku 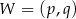 . Współrzędne wierzchołka
. Współrzędne wierzchołka 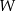 spełniają warunki
spełniają warunki
A) 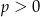 i
i 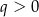 B)
B) 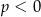 i
i 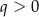 C)
C) 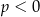 i
i 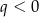 D)
D) 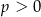 i
i 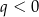
Wykres funkcji kwadratowej 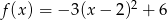 przecina oś
przecina oś 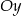 w punkcie o współrzędnych:
w punkcie o współrzędnych:
A) 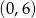 B)
B) 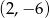 C)
C) 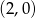 D)
D) 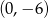
Wykres funkcji kwadratowej 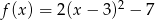 przecina oś
przecina oś 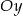 w punkcie
w punkcie
A) 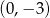 B)
B) 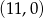 C)
C) 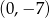 D)
D) 
Wykres funkcji kwadratowej 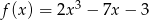 przecina oś
przecina oś 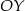 w punkcie
w punkcie
A) 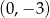 B)
B) 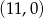 C)
C) 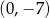 D)
D) 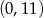
Osią symetrii wykresu funkcji 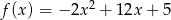 jest prosta o równaniu
jest prosta o równaniu
A) 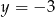 B)
B) 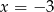 C)
C) 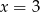 D)
D) 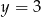
Osią symetrii wykresu funkcji kwadratowej 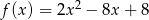 jest prosta o równaniu
jest prosta o równaniu
A) 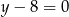 B)
B) 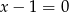 C)
C) 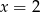 D)
D) 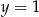
Dana jest funkcja kwadratowa 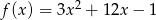 . Osią symetrii wykresu tej funkcji jest prosta
. Osią symetrii wykresu tej funkcji jest prosta
A) 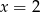 B)
B) 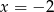 C)
C) 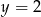 D)
D) 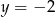
Osią symetrii paraboli o równaniu 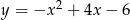 jest prosta:
jest prosta:
A) 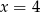 B)
B) 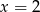 C)
C) 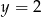 D)
D) 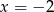
Osią symetrii wykresu funkcji kwadratowej 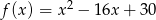 jest prosta o równaniu
jest prosta o równaniu
A) 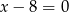 B)
B) 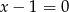 C)
C) 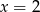 D)
D) 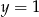
Osią symetrii wykresu funkcji 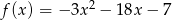 jest prosta o równaniu
jest prosta o równaniu
A) 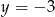 B)
B) 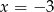 C)
C) 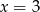 D)
D) 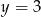
Osią symetrii wykresu funkcji 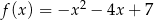 jest prosta o równaniu
jest prosta o równaniu
A) 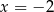 B)
B) 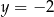 C)
C) 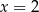 D)
D) 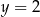
Osią symetrii wykresu funkcji kwadratowej 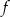 określonej wzorem
określonej wzorem 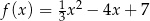 jest prosta o równaniu
jest prosta o równaniu
A) 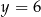 B)
B) 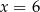 C)
C) 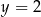 D)
D) 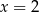
Osią symetrii wykresu funkcji kwadratowej 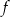 określonej wzorem
określonej wzorem 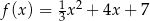 jest prosta o równaniu
jest prosta o równaniu
A) 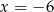 B)
B) 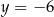 C)
C) 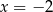 D)
D) 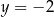
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 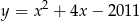 .
.
A) 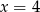 B)
B) 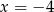 C)
C) 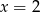 D)
D) 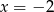
Osią symetrii wykresu funkcji 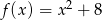 jest prosta o równaniu
jest prosta o równaniu
A) 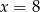 B)
B) 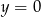 C)
C) 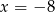 D)
D) 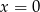
Prosta 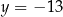 przecina wykres funkcji kwadratowej
przecina wykres funkcji kwadratowej 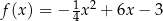 w punktach
w punktach 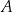 i
i 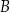 . Środek odcinka
. Środek odcinka 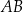 leży na prostej o równaniu
leży na prostej o równaniu
A) 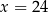 B)
B) 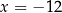 C)
C) 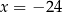 D)
D) 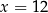
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 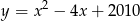 .
.
A) 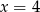 B)
B) 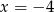 C)
C) 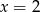 D)
D) 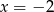
Wskaż równanie osi symetrii paraboli określonej równaniem 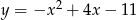 .
.
A) 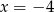 B)
B) 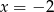 C)
C) 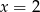 D)
D) 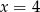
Osią symetrii wykresu funkcji kwadratowej 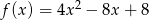 jest prosta o równaniu
jest prosta o równaniu
A) 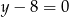 B)
B) 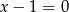 C)
C) 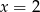 D)
D) 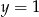
Osią symetrii wykresu funkcji kwadratowej 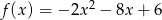 jest prosta o równaniu
jest prosta o równaniu
A) 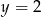 B)
B) 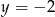 C)
C) 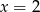 D)
D) 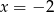
Wskaż równanie osi symetrii paraboli określonej równaniem 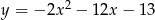 .
.
A) 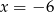 B)
B) 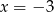 C)
C) 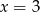 D)
D) 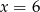
Punkt 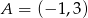 należy do wykresu funkcji
należy do wykresu funkcji 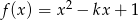 . Zatem
. Zatem 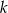 jest równe
jest równe
A) 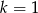 B)
B) 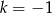 C)
C) 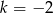 D)
D) 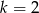
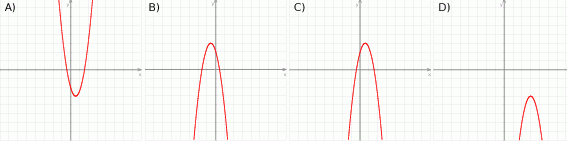
Który z rysunków może przedstawiać wykres funkcji kwadratowej 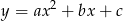 takiej, że
takiej, że 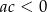 ?
?
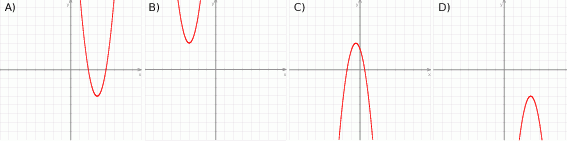
Który z rysunków może przedstawiać wykres funkcji kwadratowej 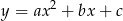 takiej, że
takiej, że 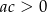 ?
?
Do wykresu funkcji 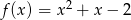 należy punkt
należy punkt
A) 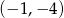 B)
B) 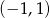 C)
C) 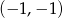 D)
D) 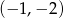
Do wykresu funkcji 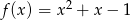 należy punkt
należy punkt
A) 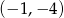 B)
B) 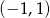 C)
C) 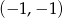 D)
D) 
Do wykresu funkcji 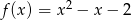 należy punkt
należy punkt
A) 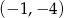 B)
B) 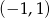 C)
C) 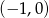 D)
D) 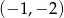
Do wykresu funkcji 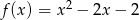 należy punkt
należy punkt
A) 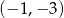 B)
B) 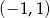 C)
C) 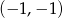 D)
D) 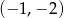
Wskaż równanie paraboli, której osią symetrii jest prosta 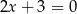 .
.
A) 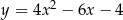 B)
B) 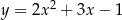
C) 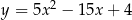 D)
D) 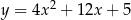
Wskaż równanie paraboli, której osią symetrii jest prosta 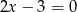 .
.
A) 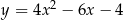 B)
B) 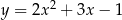
C) 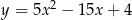 D)
D) 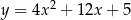
Wykresem funkcji 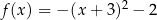 jest:
jest:
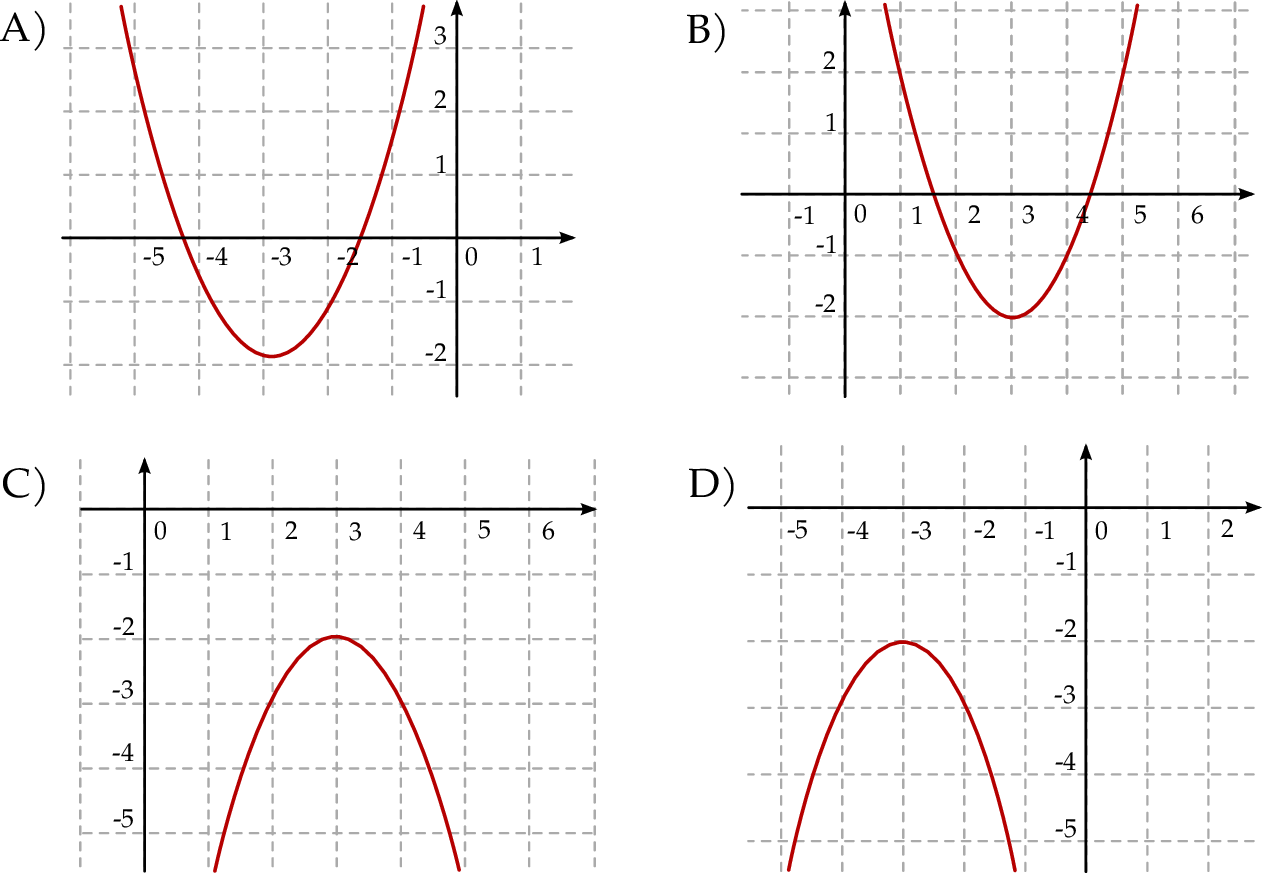
Funkcja kwadratowa 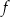 jest określona wzorem
jest określona wzorem 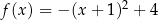 . Fragment wykresu funkcji
. Fragment wykresu funkcji 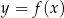 przedstawiono na rysunku
przedstawiono na rysunku
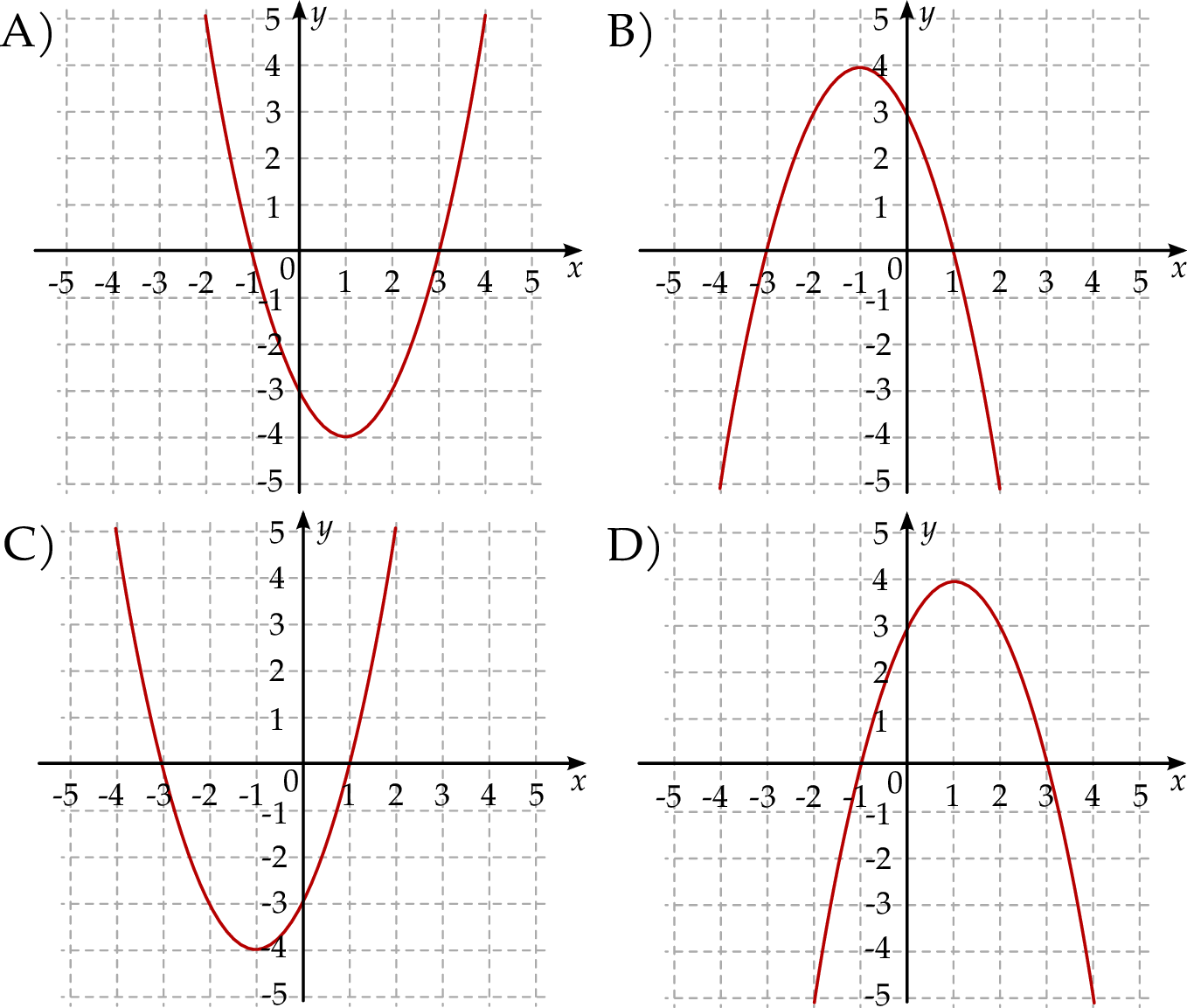
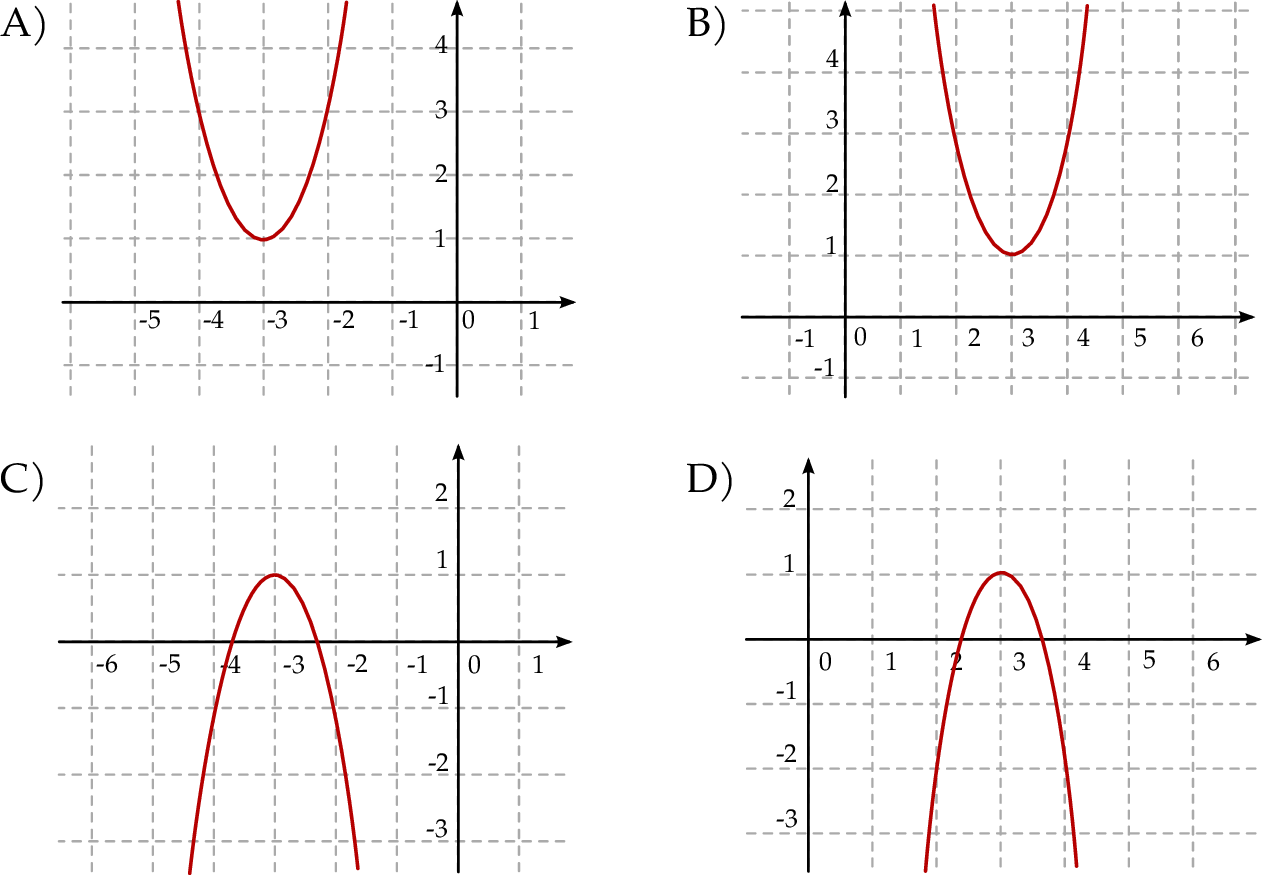
Wykres funkcji 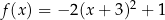 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Wierzchołek paraboli będącej wykresem funkcji 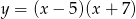 ma współrzędne
ma współrzędne
A) 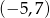 B)
B) 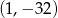 C)
C) 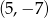 D)
D) 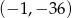
Wierzchołek paraboli będącej wykresem funkcji 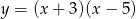 ma współrzędne
ma współrzędne
A) 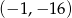 B)
B) 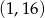 C)
C) 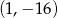 D)
D) 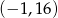
Współrzędne wierzchołka paraboli będącej wykresem funkcji 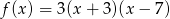 są równe
są równe
A) 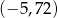 B)
B) 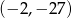 C)
C) 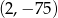 D)
D) 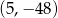
Współrzędne wierzchołka paraboli będącej wykresem funkcji 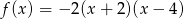 są równe
są równe
A) 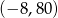 B)
B) 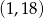 C)
C) 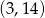 D)
D) 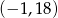
Wierzchołek paraboli będącej wykresem funkcji 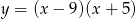 ma współrzędne
ma współrzędne
A) 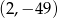 B)
B) 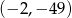 C)
C) 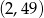 D)
D) 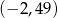
Współrzędne wierzchołka paraboli będącej wykresem funkcji 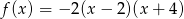 są równe
są równe
A) 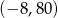 B)
B) 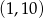 C)
C) 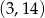 D)
D) 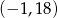
Na rysunku przedstawiono wykres funkcji kwadratowej postaci 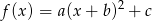 .
.
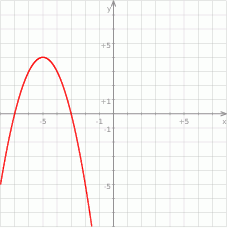
Zatem
A) 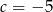 B)
B) 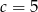 C)
C) 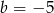 D)
D) 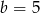
Wykres funkcji kwadratowej 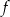 ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 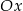 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 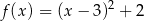 B)
B) 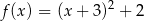
C) 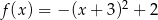 D)
D) 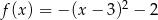
Wykres funkcji kwadratowej 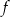 ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 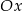 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 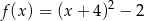 B)
B) 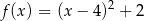
C) 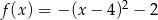 D)
D) 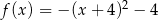
Wykres funkcji kwadratowej 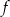 ma dwa punkty wspólne z osią
ma dwa punkty wspólne z osią 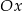 . Wskaż wzór tej funkcji
. Wskaż wzór tej funkcji
A) 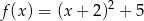 B)
B) 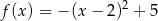
C) 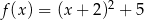 D)
D) 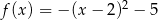
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
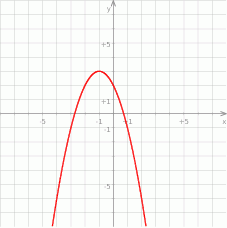
A) 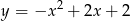 B)
B) 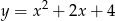 C)
C) 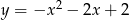 D)
D) 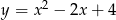
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 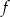 .
.
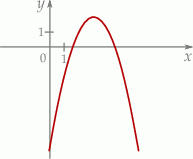
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 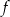 .
.
A) 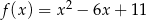 B)
B) 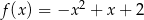
C) 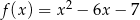 D)
D) 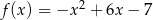
Wzorem funkcji kwadratowej 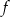 , której fragment wykresu przedstawiono na rysunku jest:
, której fragment wykresu przedstawiono na rysunku jest:
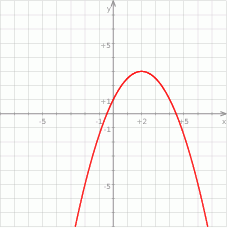
A) 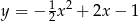 B)
B) 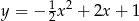 C)
C) 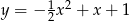 D)
D) 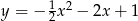
Dany jest fragment wykresu pewnej funkcji kwadratowej 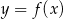 . Funkcja ta ma wzór
. Funkcja ta ma wzór
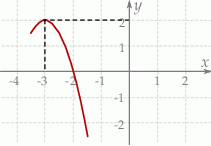
A) 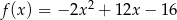 B)
B) 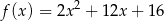
C) 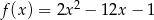 D)
D) 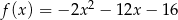
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 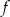 .
.
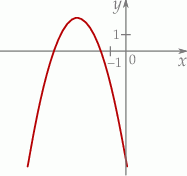
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 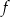 .
.
A) 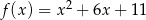 B)
B) 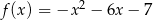
C) 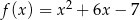 D)
D) 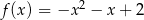
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
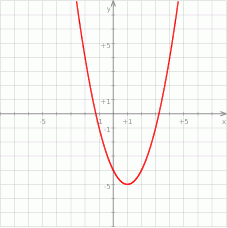
A) 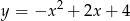 B)
B) 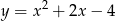 C)
C) 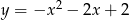 D)
D) 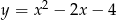
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 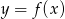 ma współrzędne
ma współrzędne 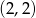 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 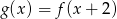 ma współrzędne
ma współrzędne
A) 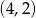 B)
B) 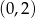 C)
C) 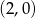 D)
D) 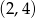
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 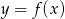 ma współrzędne
ma współrzędne 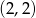 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 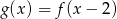 ma współrzędne
ma współrzędne
A) 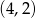 B)
B) 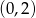 C)
C) 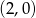 D)
D) 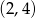
Wierzchołek paraboli o równaniu 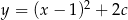 leży na prostej o równaniu
leży na prostej o równaniu 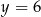 . Wtedy
. Wtedy
A) 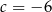 B)
B) 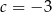 C)
C) 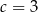 D)
D) 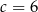
Wierzchołek paraboli o równaniu 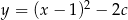 leży na prostej o równaniu
leży na prostej o równaniu 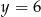 . Wtedy
. Wtedy
A) 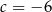 B)
B) 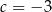 C)
C) 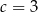 D)
D) 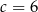
Jeśli wiadomo, że wierzchołek funkcji 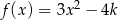 należy do prostej
należy do prostej 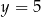 , to wartość liczbowa współczynnika
, to wartość liczbowa współczynnika 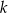 jest równa
jest równa
A) 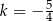 B)
B) 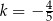 C)
C) 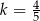 D)
D) 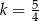
Wierzchołek paraboli o równaniu 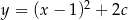 leży na prostej o równaniu
leży na prostej o równaniu 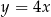 . Wtedy
. Wtedy
A) 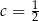 B)
B) 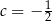 C)
C) 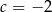 D)
D) 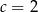
Wierzchołek paraboli o równaniu 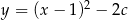 leży na prostej o równaniu
leży na prostej o równaniu 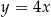 . Wtedy
. Wtedy
A) 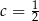 B)
B) 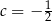 C)
C) 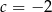 D)
D) 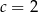
Wykresem funkcji kwadratowej 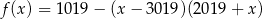 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 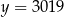 B)
B) 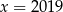 C)
C) 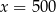 D)
D) 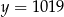
Wierzchołek paraboli o równaniu 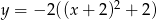 ma współrzędne
ma współrzędne
A) 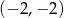 B)
B) 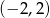 C)
C) 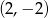 D)
D) 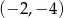
Wierzchołek paraboli o równaniu 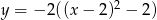 ma współrzędne
ma współrzędne
A) 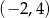 B)
B) 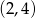 C)
C) 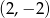 D)
D) 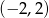
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 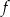 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 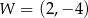 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 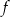 .
.
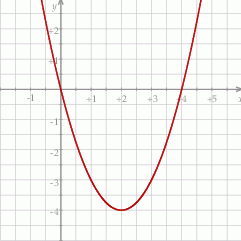
Osią symetrii wykresu funkcji 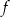 jest prosta o równaniu
jest prosta o równaniu
A) 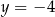 B)
B) 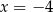 C)
C) 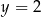 D)
D) 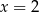
Funkcja kwadratowa 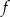 jest określona wzorem
jest określona wzorem 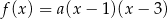 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 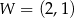 .
.
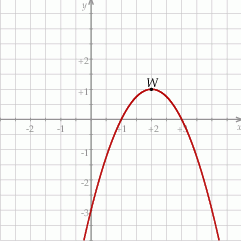
Osią symetrii paraboli będącej wykresem funkcji 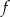 jest prosta o równaniu
jest prosta o równaniu
A) 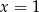 B)
B) 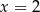 C)
C) 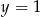 D)
D) 
W kartezjańskim układzie współrzędnych 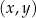 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 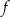 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 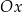 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
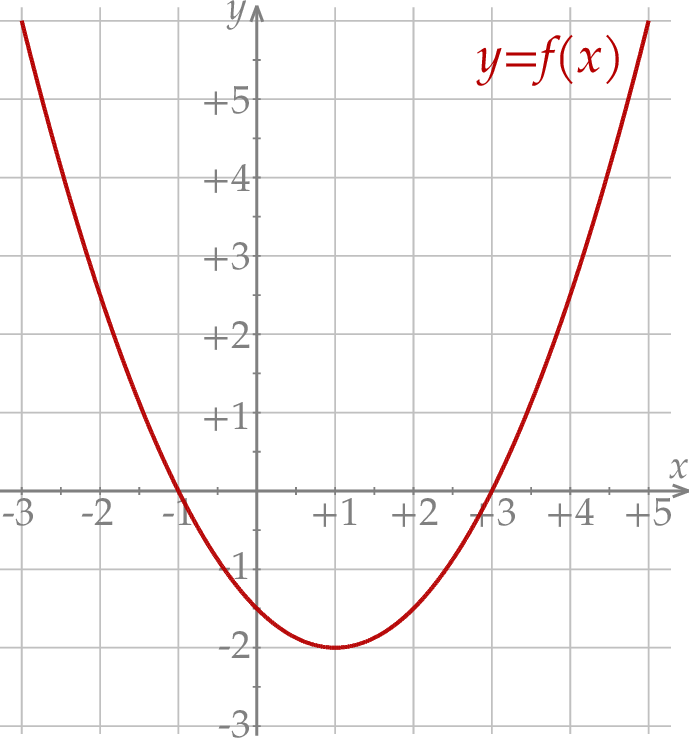
Osią symetrii wykresu funkcji 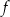 jest prosta o równaniu
jest prosta o równaniu
A) 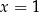 B)
B) 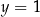 C)
C) 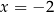 D)
D) 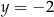
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 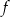 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 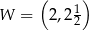 . Liczby
. Liczby 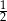 i
i 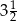 to miejsca zerowe funkcji
to miejsca zerowe funkcji 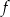 .
.
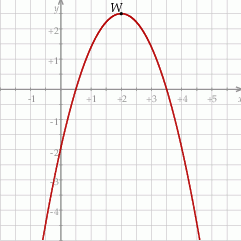
Osią symetrii wykresu funkcji 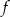 jest prosta o równaniu
jest prosta o równaniu
A) 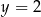 B)
B) 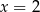 C)
C) 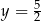 D)
D) 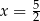
Funkcja kwadratowa 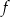 jest określona wzorem
jest określona wzorem 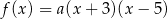 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 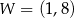 .
.
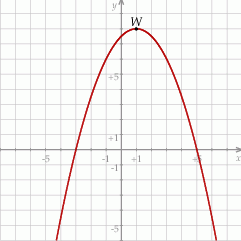
Osią symetrii paraboli będącej wykresem funkcji 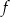 jest prosta o równaniu
jest prosta o równaniu
A) 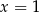 B)
B) 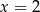 C)
C) 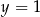 D)
D) 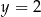
Na rysunku przedstawiono fragmenty dwóch wykresów: funkcji liniowej 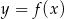 i funkcji
i funkcji ![y = g(x) = [f (x)]2](https://img.zadania.info/zad/3591919/HzadT1x.gif) . Oba wykresy przechodzą przez punkty o współrzędnych
. Oba wykresy przechodzą przez punkty o współrzędnych 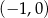 i
i 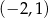 .
.
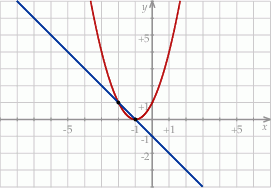
Zbiorem wartości funkcji 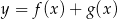 jest przedział
jest przedział
A) 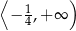 B)
B) 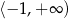 C)
C) 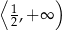 D)
D) 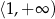
Suma współrzędnych wierzchołka paraboli 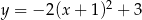 jest równa
jest równa
A) 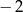 B) 2 C)
B) 2 C) 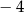 D) 4
D) 4
W kartezjańskim układzie współrzędnych 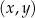 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 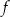 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 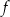 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
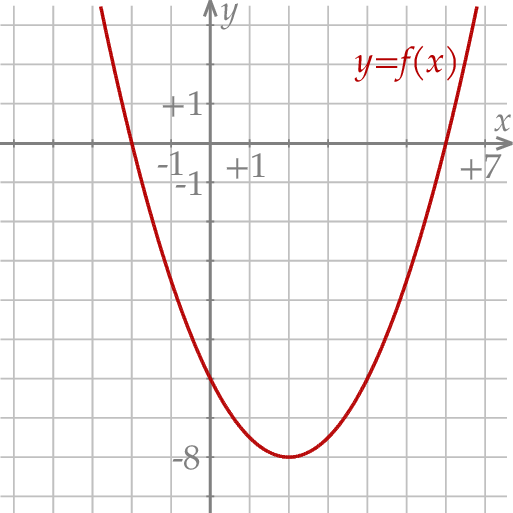
Funkcja kwadratowa 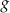 jest określona za pomocą funkcji
jest określona za pomocą funkcji 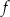 następująco:
następująco: 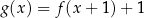 . Fragment wykresu funkcji
. Fragment wykresu funkcji 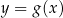 przedstawiono na rysunku
przedstawiono na rysunku