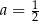Rozwiązaniem układu równań 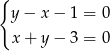 jest para
jest para
A) 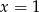 i
i 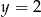 B)
B) 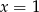 i
i 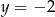 C)
C) 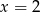 i
i 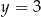 D)
D) 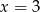 i
i 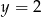
/Szkoła średnia/Zadania testowe/Równania/Układy równań
Rozwiązaniem układu równań 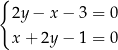 jest para
jest para
A) 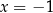 i
i 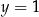 B)
B) 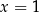 i
i 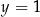 C)
C) 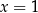 i
i 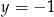 D)
D) 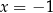 i
i 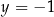
Dany jest układ równań
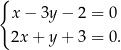
Rozwiązaniem tego układu równań jest para liczb
A) 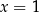 i
i 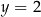 B)
B) 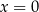 i
i 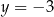 C)
C) 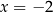 i
i 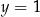 D)
D) 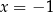 i
i 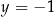
Dany jest układ równań
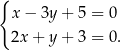
Rozwiązaniem tego układu równań jest para liczb
A) 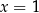 i
i 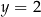 B)
B) 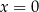 i
i 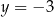 C)
C) 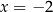 i
i 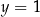 D)
D) 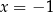 i
i 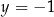
Układ równań 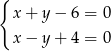 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt
A) 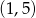 B)
B) 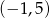 C)
C) 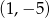 D)
D) 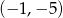
Rozwiązaniem układu równań 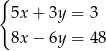 jest para liczb
jest para liczb
A) 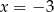 i
i 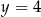 B)
B) 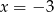 i
i 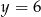 C)
C) 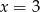 i
i 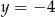 D)
D) 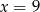 i
i 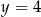
Rozwiązaniem układu równań 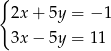 jest
jest
A) 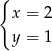 B)
B) 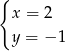 C)
C) 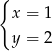 D)
D) 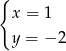
Rozwiązaniem układu równań 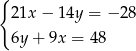 jest para liczb
jest para liczb
A) 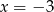 i
i 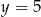 B)
B) 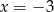 i
i 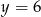 C)
C) 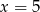 i
i 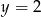 D)
D) 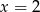 i
i 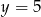
Rozwiązaniem układu równań 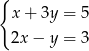 jest
jest
A) 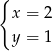 B)
B) 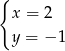 C)
C) 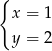 D)
D) 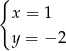
Układ równań 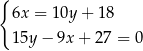
A) ma dokładnie jedno rozwiązanie. B) ma dwa rozwiązania.
C) ma nieskończenie wiele rozwiązań. D) nie ma rozwiązań.
Układ równań 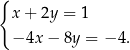
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 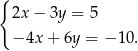
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 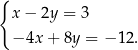
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 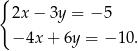
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 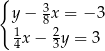
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 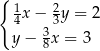
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 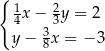
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Pary liczb 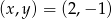 i
i 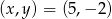 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 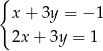 B)
B) 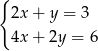 C)
C) 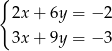 D)
D) 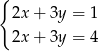
Pary liczb 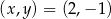 i
i 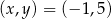 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 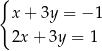 B)
B) 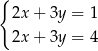 C)
C) 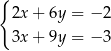 D)
D) 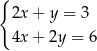
Układ liczb 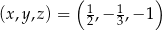 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
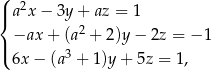
dla
A) 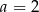 B)
B) 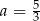 C)
C) 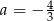 D)
D) 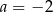
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
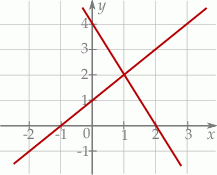
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 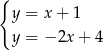 B)
B) 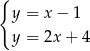 C)
C) 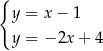 D)
D) 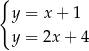
Na rysunku, w kartezjańskim układzie współrzędnych 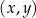 , przedstawiono interpretację geometryczną jednego z poniższych układów równań
, przedstawiono interpretację geometryczną jednego z poniższych układów równań
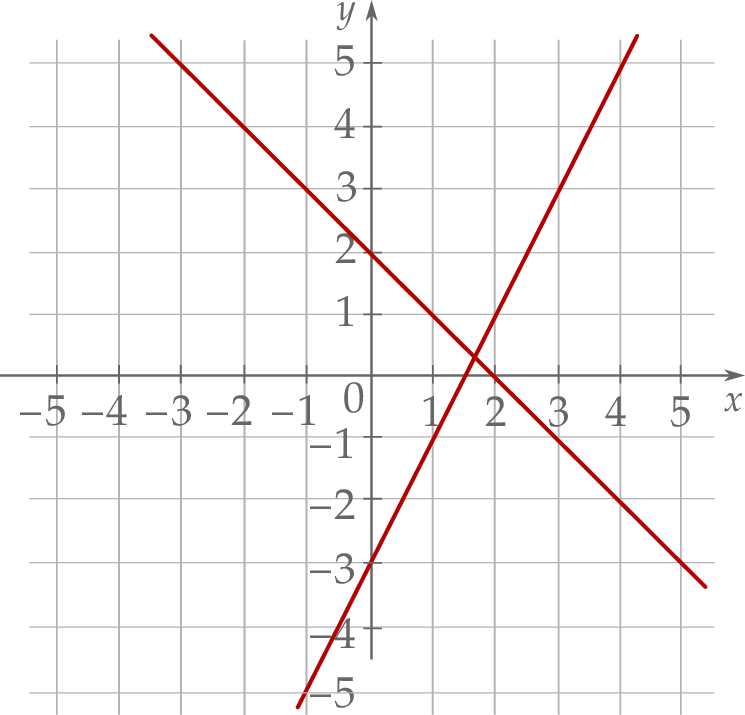
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 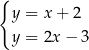 B)
B) 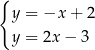 C)
C) 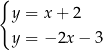 D)
D) 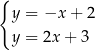
Na rysunku, w kartezjańskim układzie współrzędnych 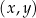 , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
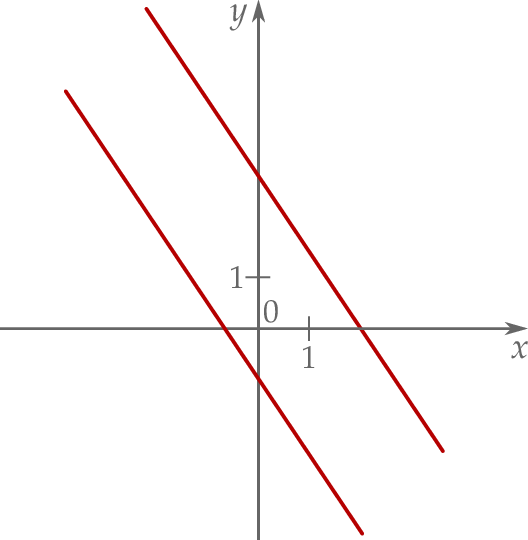
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 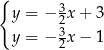 B)
B) 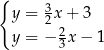
C) 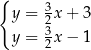 D)
D) 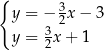
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
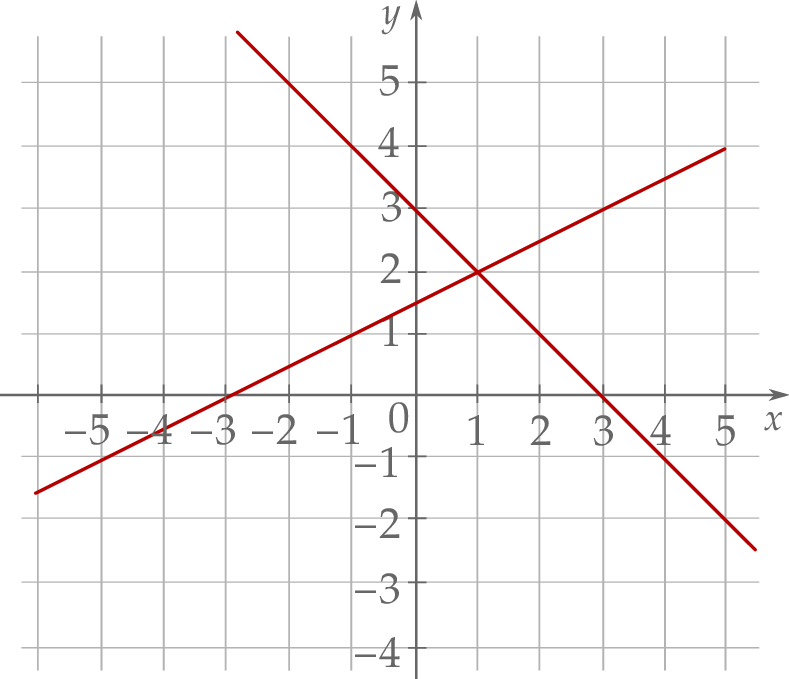
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 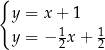 B)
B) 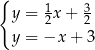 C)
C) 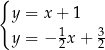 D)
D) 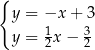
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 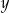 .
.
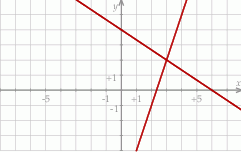
Wskaż ten układ
A) 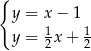 B)
B) 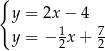 C)
C) 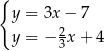 D)
D) 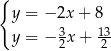
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
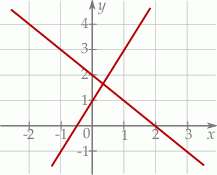
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 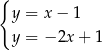 B)
B) 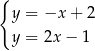 C)
C) 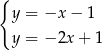 D)
D) 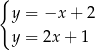
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
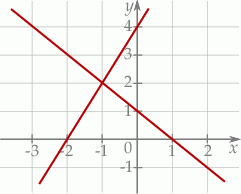
Wskaż ten układ
A) 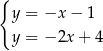 B)
B) 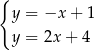 C)
C) 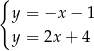 D)
D) 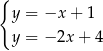
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 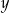 .
.
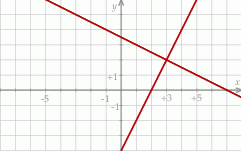
Wskaż ten układ
A) 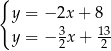 B)
B) 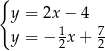 C)
C) 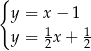 D)
D) 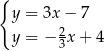
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
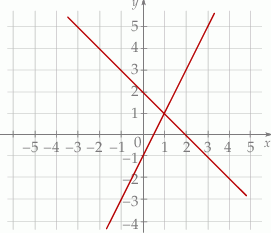
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 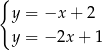 B)
B) 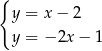 C)
C) 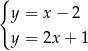 D)
D) 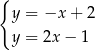
Układ równań 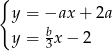 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 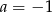 i
i 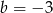 B)
B) 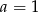 i
i 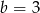 C)
C) 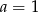 i
i 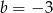 D)
D) 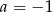 i
i 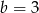
Układ równań 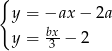 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 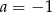 i
i 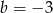 B)
B) 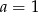 i
i 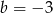 C)
C) 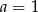 i
i 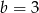 D)
D) 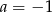 i
i 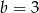
Układ równań 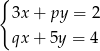 z niewiadomymi
z niewiadomymi  i
i 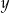 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 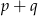 jest równa
jest równa
A) 6 B) 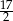 C)
C) 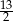 D) 15
D) 15
Układ równań 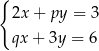 z niewiadomymi
z niewiadomymi  i
i 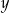 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 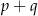 jest równa
jest równa
A) 6 B) 1 C) 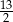 D)
D) 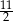
Liczby rzeczywiste 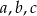 spełniają warunki:
spełniają warunki: 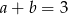 ,
, 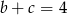 i
i 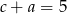 . Wtedy suma
. Wtedy suma 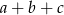 jest równa
jest równa
A) 20 B) 6 C) 4 D) 1
Liczby rzeczywiste 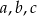 spełniają warunki:
spełniają warunki: 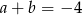 ,
, 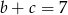 i
i 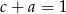 . Wtedy suma
. Wtedy suma 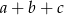 jest równa
jest równa
A) 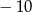 B) 8 C) 4 D) 2
B) 8 C) 4 D) 2
Jeśli 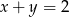 i
i 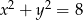 , to
, to 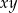 równa się
równa się
A) 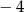 B) 2 C) 4 D)
B) 2 C) 4 D) 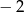
Na rysunku jest przedstawiona graficzna ilustracja układu trzech równań stopnia pierwszego z dwiema niewiadomymi  i
i 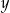 .
.
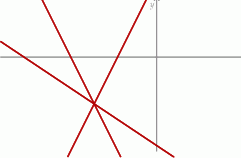
Wskaż ten układ
A) 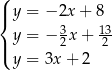 B)
B) 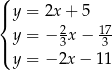 C)
C) 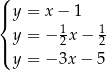 D)
D) 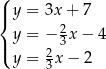
Układem sprzecznym jest układ
A) 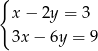 B)
B) 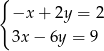 C)
C) 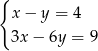 D)
D) 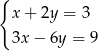
Wskaż układ, który ma nieskończenie wiele rozwiązań.
A) 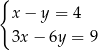 B)
B) 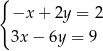 C)
C) 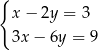 D)
D) 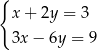
Układem sprzecznym jest układ
A) 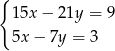 B)
B) 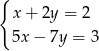 C)
C) 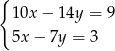 D)
D) 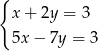
Układem sprzecznym jest układ
A) 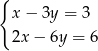 B)
B) 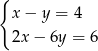 C)
C) 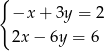 D)
D) 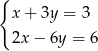
Układem sprzecznym jest układ
A) 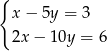 B)
B) 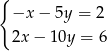 C)
C) 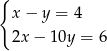 D)
D) 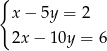
Wybierz równanie, które wraz z równaniem 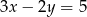 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 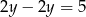 B)
B) 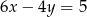 C)
C) 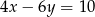 D)
D) 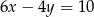
Wybierz równanie, które wraz z równaniem 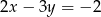 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 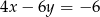 B)
B) 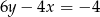 C)
C) 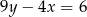 D)
D) 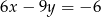
Układ równań 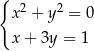 opisuje w układzie współrzędnych na płaszczyźnie
opisuje w układzie współrzędnych na płaszczyźnie
A) zbiór pusty. B) dokładnie jeden punkt.
C) dokładnie dwa różne punkty. D) zbiór nieskończony.
Jeśli 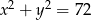 i
i 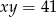 , to kwadrat sumy liczb
, to kwadrat sumy liczb 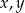 jest równy
jest równy
A) 6865 B) 154 C) 113 D) 5184
Jeśli 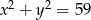 i
i 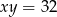 , to kwadrat sumy liczb
, to kwadrat sumy liczb 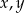 jest równy
jest równy
A) 3545 B) 91 C) 123 D) 3481
Jeśli 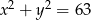 i
i 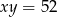 , to kwadrat sumy liczb
, to kwadrat sumy liczb 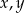 jest równy
jest równy
A) 167 B) 3969 C) 115 D) 4073
Rozwiązaniem układu równań 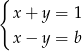 z niewiadomymi
z niewiadomymi  i
i 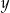 jest para liczb dodatnich. Wynika stąd, że
jest para liczb dodatnich. Wynika stąd, że
A) 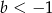 B)
B) 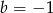 C)
C) 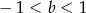 D)
D) 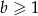
Rozwiązaniem układu równań 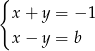 z niewiadomymi
z niewiadomymi  i
i 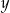 jest para liczb ujemnych. Wynika stąd, że
jest para liczb ujemnych. Wynika stąd, że
A) 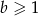 B)
B) 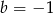 C)
C) 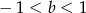 D)
D) 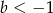
Liczby rzeczywiste 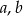 spełniają warunki:
spełniają warunki: 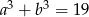 ,
, 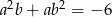 . Wtedy suma
. Wtedy suma 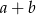 jest równa
jest równa
A) 37 B) 13 C) 1 D) 25
Jeżeli 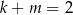 i
i 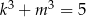 , to wartość iloczynu
, to wartość iloczynu 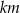 jest równa
jest równa
A)  B)
B) 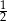 C)
C)  D)
D) 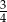
Ile rozwiązań ma układ równań 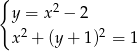 ?
?
A) 0 B) 1 C) 2 D) 3
Ile rozwiązań ma układ równań 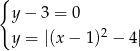
A) 1 B) 2 C) 3 D) 4
Ile rozwiązań ma układ równań 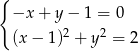 ?
?
A) 0 B) 1 C) 2 D) 3
Para liczb 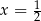 i
i 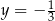 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 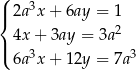 dla
dla
A) 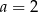 B)
B) 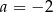 C)
C) 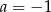 D)
D)