Ciągiem arytmetycznym jest ciąg o wyrazie ogólnym 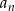 równym:
równym:
A) 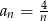 B)
B) 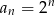 C)
C) 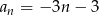 D)
D) 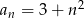
/Szkoła średnia/Zadania testowe/Ciągi
W ciągu arytmetycznym 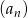 pierwszy wyraz jest równy
pierwszy wyraz jest równy 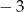 , zaś
, zaś 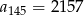 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba
A) 13 B) 14 C) 15 D) 16
W ciągu arytmetycznym 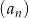 pierwszy wyraz jest równy 45, zaś
pierwszy wyraz jest równy 45, zaś 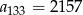 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba
A) 13 B) 14 C) 15 D) 16
W ciągu arytmetycznym 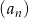 pierwszy wyraz jest równy 32, zaś
pierwszy wyraz jest równy 32, zaś 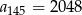 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba
A) 13 B) 14 C) 15 D) 16
Który wyraz ciągu 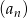 o wyrazie ogólnym
o wyrazie ogólnym 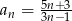 jest równy 2?
jest równy 2?
A) piąty B) siedemnasty C) siódmy D) dziewiąty
Który wyraz ciągu 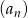 o wyrazie ogólnym
o wyrazie ogólnym 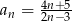 jest równy 3?
jest równy 3?
A) piąty B) siedemnasty C) siódmy D) dziewiąty
Dany jest ciąg o wzorze ogólnym 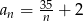 . Wartość
. Wartość  ma wyraz
ma wyraz
A) szesnasty B) trzydziesty pierwszy C) siedemdziesiąty D) osiemnasty
Ciąg 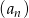 określony jest wzorem
określony jest wzorem 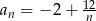 dla
dla 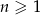 . Równość
. Równość 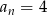 zachodzi dla
zachodzi dla
A) 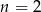 B)
B) 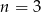 C)
C) 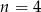 D)
D) 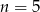
Który z podanych ciągów jest ciągiem geometrycznym?
A) 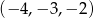 B)
B) 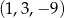 C)
C) 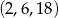 D)
D) 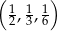
Ile wyrazów równych zero ma nieskończony ciąg 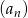 o wyrazie ogólnym
o wyrazie ogólnym
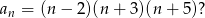
A) 0 B) 1 C) 2 D) 3
Ile wyrazów równych zero ma nieskończony ciąg 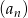 o wyrazie ogólnym
o wyrazie ogólnym
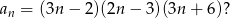
A) 0 B) 1 C) 2 D) 3
Ile wyrazów równych zero ma nieskończony ciąg 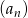 o wyrazie ogólnym
o wyrazie ogólnym
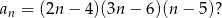
A) 0 B) 1 C) 2 D) 3
Ciąg 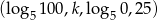 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 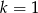 B)
B) 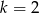 C)
C) 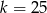 D)
D) 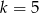
Ciąg 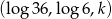 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 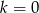 B)
B) 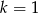 C)
C) 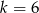 D)
D) 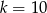
Ciąg 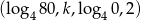 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 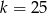 B)
B) 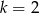 C)
C) 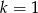 D)
D) 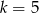
Ciągiem geometrycznym o ilorazie 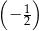 jest ciąg określony wzorem
jest ciąg określony wzorem
A) 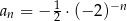 B)
B) 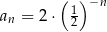 C)
C) 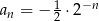 D)
D) 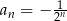
W ciągu arytmetycznym 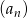 wyraz
wyraz 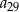 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 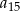 oraz
oraz 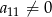 . Wtedy iloraz
. Wtedy iloraz 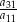 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
W ciągu arytmetycznym 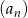 wyraz
wyraz 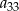 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 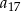 oraz
oraz 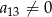 . Wtedy iloraz
. Wtedy iloraz 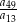 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 5 dają resztę 3. Dziesiąty wyraz tego ciągu jest równy
A) 43 B) 53 C) 58 D) 68
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 7 dają resztę 4. Dziewiąty wyraz tego ciągu jest równy
A) 53 B) 74 C) 60 D) 67
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 4 dają resztę 3. Dwunasty wyraz tego ciągu jest równy
A) 51 B) 55 C) 59 D) 63
Dany jest ciąg 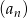 jest określony wzorem
jest określony wzorem 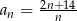 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 5 B) 4 C) 3 D) 2
Dany jest ciąg 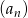 jest określony wzorem
jest określony wzorem 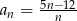 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 6 B) 4 C) 3 D) 7
Ciąg 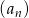 jest określony wzorem
jest określony wzorem 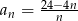 dla
dla 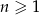 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 7 B) 6 C) 5 D) 4
Dany jest ciąg 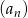 jest określony wzorem
jest określony wzorem 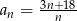 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 5 B) 4 C) 8 D) 6
Ciąg 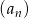 jest określony wzorem
jest określony wzorem 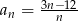 dla
dla 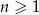 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 6 B) 4 C) 3 D) 2
Dany jest ciąg 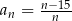 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 0 B) 1 C) 3 D) 4
Ciąg geometryczny określony jest wzorem 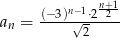 , dla
, dla 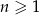 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 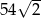 B)
B) 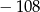 C)
C) 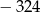 D)
D) 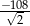
Dany jest nieskończony ciąg geometryczny 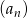 , w którym
, w którym 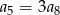 . Wtedy
. Wtedy
A) 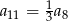 B)
B) 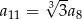 C)
C) 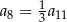 D)
D) 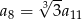
Dany jest nieskończony ciąg geometryczny 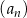 , w którym
, w którym 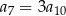 . Wtedy
. Wtedy
A) 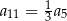 B)
B) 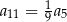 C)
C) 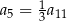 D)
D) 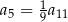
Wszystkie wyrazy nieskończonego ciągu geometrycznego 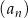 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 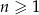 , są dodatnie i
, są dodatnie i 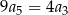 . Wtedy iloraz tego ciągu jest równy
. Wtedy iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 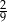 D)
D) 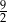
Ciąg 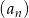 jest określony wzorem
jest określony wzorem 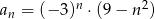 dla
dla 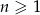 . Wynika stąd, że
. Wynika stąd, że
A) 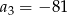 B)
B) 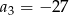 C)
C) 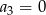 D)
D) 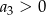
Dla 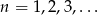 ciąg
ciąg 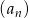 jest określony wzorem
jest określony wzorem 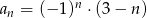 . Wtedy
. Wtedy
A) 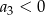 B)
B) 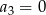 C)
C) 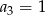 D)
D) 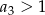
Ciąg 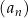 jest określony wzorem
jest określony wzorem 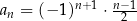 dla każdej liczby naturalnej
dla każdej liczby naturalnej 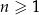 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 2 B) 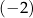 C) 3 D)
C) 3 D) 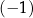
Ciąg 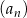 jest określony wzorem
jest określony wzorem 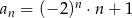 dla każdej liczby naturalnej
dla każdej liczby naturalnej 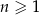 . Wtedy trzeci wyraz tego ciągu jest równy
. Wtedy trzeci wyraz tego ciągu jest równy
A) 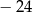 B)
B) 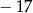 C)
C) 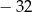 D)
D) 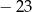
Ciąg 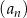 jest określony wzorem
jest określony wzorem 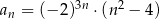 dla
dla 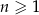 . Wówczas
. Wówczas
A) 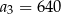 B)
B) 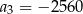 C)
C) 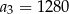 D)
D) 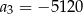
Ciąg 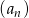 jest określony wzorem
jest określony wzorem 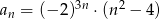 dla
dla 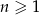 . Wówczas
. Wówczas
A) 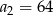 B)
B) 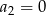 C)
C) 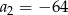 D)
D) 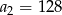
Ciąg 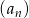 jest określony wzorem
jest określony wzorem 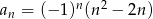 dla
dla 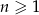 . Wtedy
. Wtedy
A) 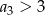 B)
B) 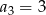 C)
C) 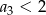 D)
D) 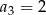
Ciąg 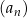 jest określony wzorem
jest określony wzorem 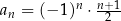 dla każdej liczby naturalnej
dla każdej liczby naturalnej 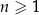 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 2 B) 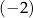 C) 3 D)
C) 3 D) 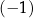
Ciąg 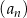 jest określony wzorem
jest określony wzorem 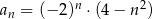 , dla
, dla 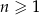 . Wtedy
. Wtedy
A) 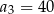 B)
B) 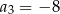 C)
C) 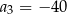 D)
D) 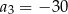
Dla 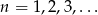 ciąg
ciąg 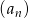 jest określony wzorem
jest określony wzorem 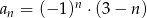 . Wtedy
. Wtedy
A) 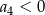 B)
B) 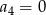 C)
C) 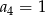 D)
D) 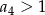
Ciąg 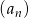 jest określony wzorem
jest określony wzorem 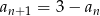 dla każdej liczby naturalnej
dla każdej liczby naturalnej 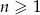 . Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
. Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
A) 150 B) 75 C) 50 D) 100
Dwa kolejne wyrazy ciągu geometrycznego 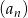 są równe 3 i 18. Wyrazem tego ciągu może być liczba
są równe 3 i 18. Wyrazem tego ciągu może być liczba
A) 27 B) 54 C) 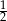 D)
D) 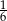
Dwa kolejne wyrazy ciągu geometrycznego 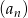 są równe 4 i 24. Wyrazem tego ciągu może być liczba
są równe 4 i 24. Wyrazem tego ciągu może być liczba
A) 96 B) 108 C) 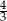 D)
D) 
Dwa kolejne wyrazy ciągu geometrycznego 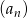 są równe 9 i 15. Wyrazem tego ciągu może być liczba
są równe 9 i 15. Wyrazem tego ciągu może być liczba
A) 6,25 B) 21 C) 24,5 D) 5,4
Ciągiem geometrycznym jest ciąg określony wzorem
A) 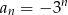 B)
B) 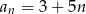 C)
C) 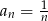 D)
D) 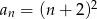
Którym wzorem ogólnym przedstawiono ciąg geometryczny?
A) 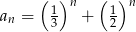 B)
B) 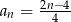 C)
C) 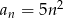 D)
D) 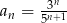
Ciągiem geometrycznym jest ciąg określony wzorem
A) 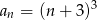 B)
B) 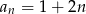 C)
C) 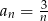 D)
D) 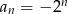
Ciągiem geometrycznym jest ciąg określony wzorem
A) 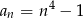 B)
B) 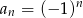 C)
C) 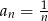 D)
D) 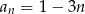
Ciągiem geometrycznym jest ciąg określony wzorem
A) 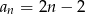 B)
B) 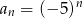 C)
C) 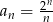 D)
D) 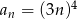
Ciągiem geometrycznym jest ciąg określony wzorem
A) 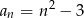 B)
B) 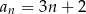 C)
C) 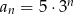 D)
D) 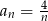
Granica ciągu 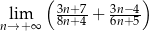 jest równa
jest równa
A) 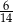 B)
B)  C)
C) 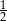 D)
D) 
Granica ciągu 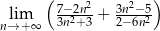 jest równa
jest równa
A) 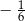 B)
B)  C)
C) 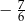 D)
D) 
Iloraz nieskończonego ciągu geometrycznego 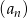 jest równy
jest równy 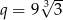 . Wynika stąd, że
. Wynika stąd, że
A) 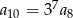 B)
B) 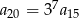 C)
C) 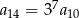 D)
D) 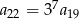
Dany jest ciąg 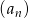 o wyrazie ogólnym
o wyrazie ogólnym 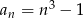 , gdzie
, gdzie 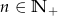 . Wówczas:
. Wówczas:
A) 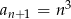 B)
B) 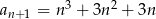 C)
C) 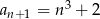 D)
D) 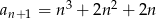
Dany jest ciąg 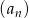 o wyrazie ogólnym
o wyrazie ogólnym 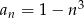 , gdzie
, gdzie 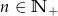 . Wówczas:
. Wówczas:
A) 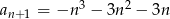
B) 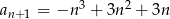
C) 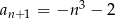
D) 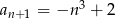
Dany jest ciąg 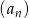 o wyrazie ogólnym
o wyrazie ogólnym 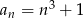 , gdzie
, gdzie 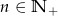 . Wówczas:
. Wówczas:
A) 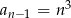 B)
B) 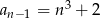 C)
C) 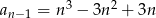 D)
D) 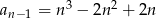
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 16 B) -16 C) 8 D) -8
W ciągu geometrycznym 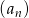 mamy
mamy 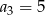 i
i 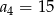 . Wtedy wyraz
. Wtedy wyraz 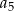 jest równy
jest równy
A) 10 B) 20 C) 75 D) 45
W ciągu geometrycznym 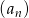 , gdzie
, gdzie 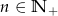 dane są:
dane są: 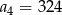 i
i 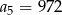 . Zatem:
. Zatem:
A) 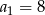 B)
B) 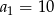 C)
C) 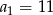 D)
D) 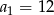
Dany jest nieskończony ciąg geometryczny 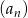 , w którym
, w którym 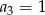 i
i 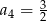 . Wtedy
. Wtedy
A) 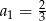 B)
B) 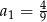 C)
C) 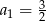 D)
D) 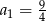
W ciągu geometrycznym 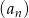 mamy
mamy 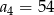 i
i 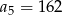 . Wtedy wyraz
. Wtedy wyraz 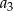 jest równy
jest równy
A) 6 B) 18 C) 2 D) 27
Trzeci wyraz ciągu geometrycznego jest równy 6, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 27 B) -27 C) 54 D) -54
Dany jest nieskończony ciąg geometryczny 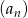 , w którym
, w którym 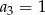 i
i 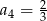 . Wtedy
. Wtedy
A) 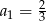 B)
B) 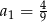 C)
C) 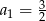 D)
D) 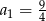
Jeśli trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy 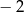 , to drugi wyraz jest równy
, to drugi wyraz jest równy
A) 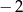 B) 2 C)
B) 2 C) 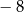 D) 8
D) 8

