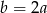Wielomian 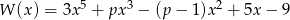 jest podzielny przez dwumian
jest podzielny przez dwumian 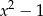 dla
dla 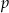 równego
równego
A) 6 B) 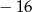 C) 4 D)
C) 4 D) 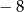
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany/Z parametrem
Wielomiany 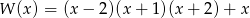 i
i 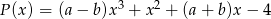 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 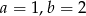 B)
B) 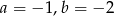 C)
C) 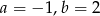 D)
D) 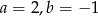
Wielomiany 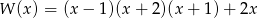 i
i 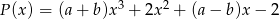 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 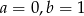 B)
B) 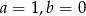 C)
C) 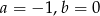 D)
D) 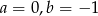
Wielomiany 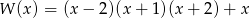 i
i 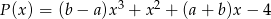 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 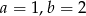 B)
B) 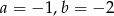 C)
C) 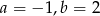 D)
D) 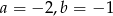
Wielomian 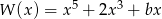 jest podzielny przez wielomian
jest podzielny przez wielomian 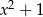 . Wynika stąd, że
. Wynika stąd, że
A) 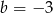 B)
B) 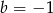 C)
C) 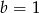 D)
D) 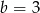
Wielomian 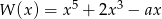 jest podzielny przez wielomian
jest podzielny przez wielomian 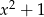 . Wynika stąd, że
. Wynika stąd, że
A) 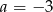 B)
B) 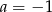 C)
C) 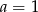 D)
D) 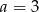
Wielomiany 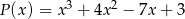 i
i 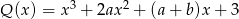 są równe. Zatem
są równe. Zatem
A) 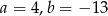 B)
B) 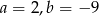 C)
C) 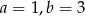 D)
D) 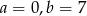
Wielomiany 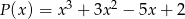 i
i 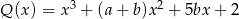 są równe. Zatem
są równe. Zatem
A) 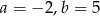 B)
B) 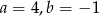 C)
C) 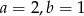 D)
D) 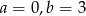
Wielomian 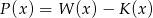 jest siódmego stopnia oraz
jest siódmego stopnia oraz 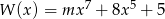 ,
, 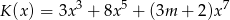 . Wynika stąd, że liczba
. Wynika stąd, że liczba 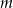 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Wielomian 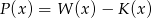 jest piątego stopnia oraz
jest piątego stopnia oraz 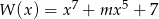 ,
, 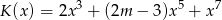 . Wynika stąd, że liczba
. Wynika stąd, że liczba 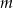 jest różna od
jest różna od
A) 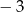 B)
B) 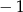 C) 1 D) 3
C) 1 D) 3
Wielomian 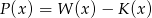 jest siódmego stopnia oraz
jest siódmego stopnia oraz 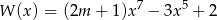 ,
, 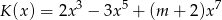 . Wynika stąd, że liczba
. Wynika stąd, że liczba 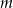 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Reszta z dzielenia wielomianu 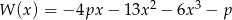 przez dwumian
przez dwumian 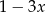 jest równa 3. Zatem
jest równa 3. Zatem
A) 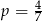 B)
B) 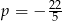 C)
C) 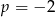 D)
D) 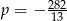
Wielomiany 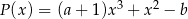 i
i 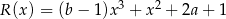 są równe. Zatem liczba
są równe. Zatem liczba 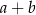
A) należy do zbioru 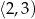 B) jest większa od 3
B) jest większa od 3
C) należy do zbioru 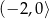 D) jest mniejsza od -2
D) jest mniejsza od -2
Wielomian 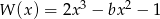 jest podzielny przez dwumian
jest podzielny przez dwumian 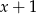 . Wynika stąd, że
. Wynika stąd, że
A) 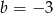 B)
B) 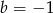 C)
C) 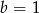 D)
D) 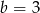
Wielomian 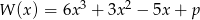 jest podzielny przez dwumian
jest podzielny przez dwumian 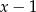 dla
dla 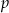 równego
równego
A) 4 B) 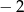 C) 2 D)
C) 2 D) 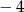
Wielomian 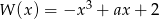 jest podzielny przez dwumian
jest podzielny przez dwumian 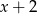 . Wynika stąd, że
. Wynika stąd, że
A) 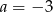 B)
B) 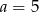 C)
C) 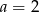 D)
D) 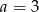
Wielomian 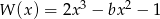 jest podzielny przez dwumian
jest podzielny przez dwumian 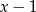 . Wynika stąd, że
. Wynika stąd, że
A) 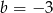 B)
B) 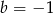 C)
C) 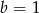 D)
D) 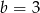
Reszta z dzielenia wielomianu 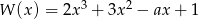 przez dwumian
przez dwumian 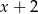 jest równa
jest równa 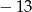 . Zatem
. Zatem
A) 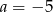 B)
B) 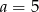 C)
C) 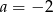 D)
D) 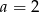
Reszta z dzielenia wielomianu 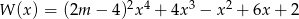 przez dwumian
przez dwumian 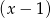 jest równa 11 dla
jest równa 11 dla
A) 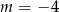 B)
B) 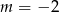 C)
C) 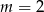 D)
D) 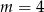
Reszta z dzielenia wielomianu 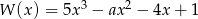 przez dwumian
przez dwumian 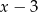 jest równa 88. Zatem
jest równa 88. Zatem
A) 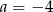 B)
B) 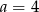 C)
C) 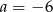 D)
D) 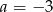
Wielomian 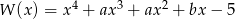 jest podzielny przez wielomian
jest podzielny przez wielomian 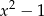 . Wynika stąd, że
. Wynika stąd, że
A) 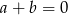 B)
B) 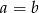 C)
C) 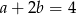 D)
D)