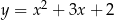Wykres funkcji 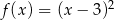 przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
A) 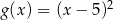 B)
B) 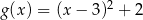 C)
C) 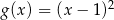 D)
D) 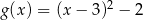
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Przesunięcie
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 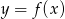 ma współrzędne
ma współrzędne 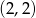 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 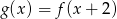 ma współrzędne
ma współrzędne
A) 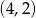 B)
B) 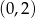 C)
C) 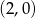 D)
D) 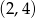
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 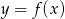 ma współrzędne
ma współrzędne 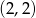 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 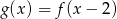 ma współrzędne
ma współrzędne
A) 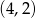 B)
B) 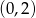 C)
C) 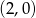 D)
D) 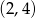
Wskaż wzór funkcji, której wykres można otrzymać przez przesunięcie wykresu funkcji 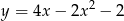 .
.
A) 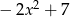 B)
B) 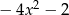 C)
C) 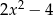 D)
D) 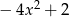
Funkcja kwadratowa 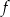 jest określona wzorem
jest określona wzorem 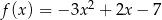 . Jeżeli przesuniemy wykres funkcji
. Jeżeli przesuniemy wykres funkcji 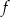 o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
o dwie jednostki 2 lewo, to otrzymamy wykres funkcji
A) 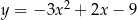 B)
B) 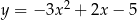
C) 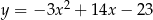 D)
D) 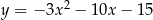
Wykres funkcji kwadratowej 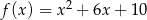 powstaje z wykresu funkcji
powstaje z wykresu funkcji 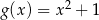 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Wykres funkcji kwadratowej 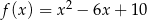 powstaje z wykresu funkcji
powstaje z wykresu funkcji 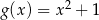 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Funkcja kwadratowa 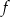 określona jest wzorem
określona jest wzorem 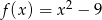 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 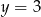 , należy go przesunąć o
, należy go przesunąć o
A) 12 jednostek w prawo wzdłuż osi 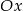
B) 12 jednostek do góry wzdłuż osi 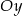
C) 12 jednostek do dołu wzdłuż osi 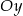
D) 3 jednostki w lewo wzdłuż osi 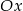
Funkcja kwadratowa 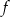 określona jest wzorem
określona jest wzorem 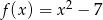 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 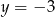 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 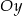
B) 10 jednostek do góry wzdłuż osi 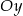
C) 4 jednostki w dół wzdłuż osi 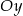
D) 10 jednostek w dół wzdłuż osi 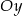
Funkcja kwadratowa 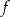 określona jest wzorem
określona jest wzorem 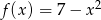 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 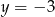 , należy go przesunąć o
, należy go przesunąć o
A) 4 jednostki do góry wzdłuż osi 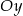
B) 10 jednostek do góry wzdłuż osi 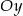
C) 4 jednostki w dół wzdłuż osi 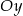
D) 10 jednostek w dół wzdłuż osi 
Funkcja 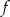 określona jest wzorem
określona jest wzorem 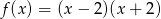 . Funkcja
. Funkcja 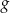 określona jest wzorem
określona jest wzorem 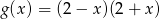 . Wykres funkcji
. Wykres funkcji 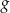 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 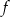
A) przesuwając go o 2 jednostki w dół wzdłuż osi 
B) przesuwając go o 2 jednostki w lewo wzdłuż osi 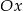
C) w symetrii względem osi 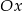
D) w symetrii względem osi 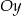
Funkcja 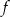 określona jest wzorem
określona jest wzorem 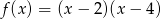 . Funkcja
. Funkcja 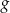 określona jest wzorem
określona jest wzorem 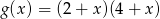 . Wykres funkcji
. Wykres funkcji 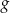 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 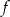
A) przesuwając go o 3 jednostki w dół wzdłuż osi 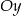
B) przesuwając go o 3 jednostki w lewo wzdłuż osi 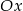
C) w symetrii względem osi 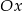
D) w symetrii względem osi 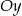
Funkcja 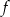 określona jest wzorem
określona jest wzorem 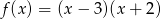 . Funkcja
. Funkcja 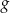 określona jest wzorem
określona jest wzorem 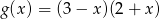 . Wykres funkcji
. Wykres funkcji 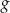 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 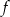
A) w symetrii względem osi 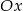
B) przesuwając go o 2 jednostki w lewo wzdłuż osi 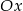
C) przesuwając go o 4 jednostki w dół wzdłuż osi 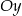
D) w symetrii względem osi 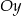
Gdy przesuniemy wykres funkcji 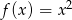 o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
A) 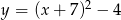 B)
B) 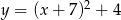 C)
C) 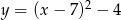 D)
D) 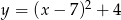
Wykres funkcji 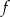 określonej wzorem
określonej wzorem 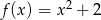 przesuwamy o 4 jednostki w dół wzdłuż osi
przesuwamy o 4 jednostki w dół wzdłuż osi 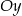 i o 2 jednostki w prawo wzdłuż osi
i o 2 jednostki w prawo wzdłuż osi 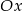 . Otrzymujemy w ten sposób wykres funkcji
. Otrzymujemy w ten sposób wykres funkcji 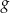 określonej wzorem
określonej wzorem
A) 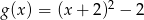
B) 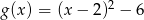
C) 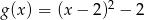
D) 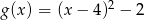
Wykres funkcji 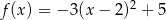 przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 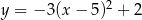 B)
B) 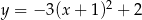
C) 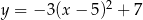 D)
D) 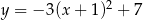
Wykres funkcji 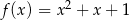 przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 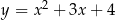 B)
B) 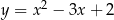
C) 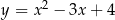 D)
D)