Dane są wielomiany 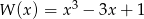 oraz
oraz 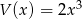 . Wielomian
. Wielomian 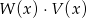 jest równy
jest równy
A) 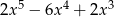 B)
B) 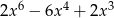 C)
C) 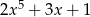 D)
D) 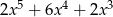
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany/Iloczyn
Dane są wielomiany 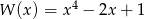 oraz
oraz 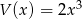 . Wielomian
. Wielomian 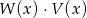 jest równy
jest równy
A) 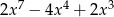 B)
B) 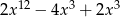 C)
C) 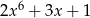 D)
D) 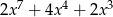
Dane są wielomiany 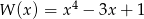 oraz
oraz 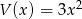 . Wielomian
. Wielomian 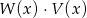 jest równy
jest równy
A) 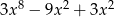 B)
B) 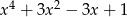 C)
C) 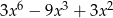 D)
D) 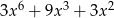
Dane są wielomiany 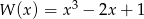 oraz
oraz 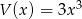 . Wielomian
. Wielomian 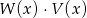 jest równy
jest równy
A) 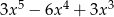 B)
B) 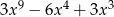 C)
C) 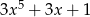 D)
D) 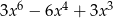
Iloczyn wielomianów 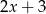 oraz
oraz 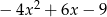 jest równy
jest równy
A) 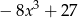 B)
B) 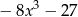 C)
C) 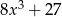 D)
D) 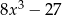
Iloczyn wielomianów 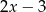 oraz
oraz 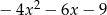 jest równy
jest równy
A) 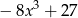 B)
B) 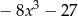 C)
C) 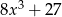 D)
D) 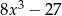
Iloczyn wielomianów 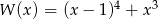 i
i 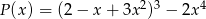 jest wielomianem stopnia
jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7
Dane są wielomiany 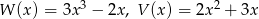 . Stopień wielomianu
. Stopień wielomianu 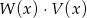 jest równy
jest równy
A) 6 B) 5 C) 4 D) 3
Dane są wielomiany 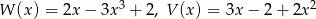 . Stopień wielomianu
. Stopień wielomianu 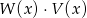 jest równy
jest równy
A) 6 B) 4 C) 5 D) 3
Wielomian 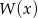 jest iloczynem wielomianów
jest iloczynem wielomianów 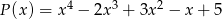 i
i 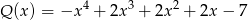 . Zatem stopień wielomianu
. Zatem stopień wielomianu 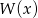 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Dane są dwa wielomiany 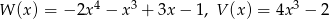 . Stopień wielomianu
. Stopień wielomianu 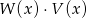 jest równy
jest równy
A) 12 B) 7 C) 4 D) 3
Iloczyn wielomianów 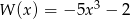 i
i 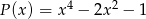 jest wielomianem stopnia
jest wielomianem stopnia
A) 7 B) 3 C) 5 D) 6
Iloczyn wielomianów 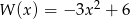 i
i 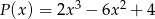 jest wielomianem stopnia
jest wielomianem stopnia
A) 2 B) 3 C) 5 D) 6
Dane są wielomiany: 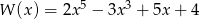 i
i 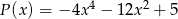 . Stopień wielomianu
. Stopień wielomianu 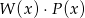 jest równy:
jest równy:
A) 20 B) -8 C) 9 D) 5
Dane są wielomiany: 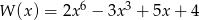 i
i 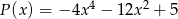 . Stopień wielomianu
. Stopień wielomianu 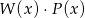 jest równy:
jest równy:
A) 24 B) 10 C) 9 D) 6
Dane są wielomiany 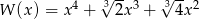 oraz
oraz 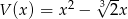 . Wielomian
. Wielomian 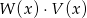 jest równy
jest równy
A) 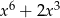 B)
B) 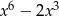 C)
C) 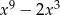 D)
D) 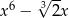
Aby otrzymać wielomian 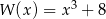 , należy pomnożyć wielomian
, należy pomnożyć wielomian 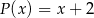 przez wielomian:
przez wielomian:
A) 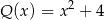 B)
B) 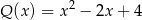
C) 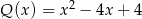 D)
D) 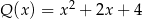
Przez jaki wielomian należy pomnożyć 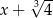 aby otrzymać wielomian
aby otrzymać wielomian 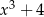 ?
?
A) 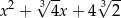 B)
B) 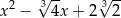
C) 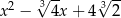 D)
D) 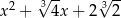
Iloczyn dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego

