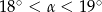Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 3:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 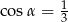 B)
B) 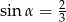 C)
C) 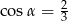 D)
D) 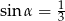
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek/Kąty
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 5:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 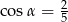 B)
B) 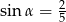 C)
C) 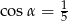 D)
D) 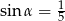
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 8:6. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 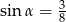 B)
B) 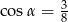 C)
C) 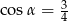 D)
D) 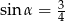
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
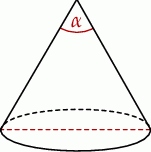
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 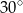 B)
B) 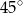 C)
C) 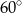 D)
D) 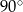
Tworząca stożka o wysokości 3 ma długość 6 (zobacz rysunek).
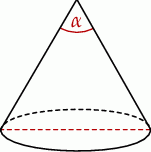
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 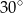 B)
B) 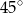 C)
C) 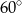 D)
D) 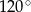
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 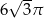 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 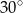 B)
B) 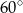 C)
C) 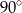 D)
D) 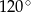
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 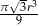 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 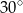 B)
B) 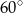 C)
C) 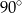 D)
D) 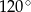
Średnica podstawy stożka ma długość 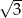 , a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
, a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
A) 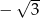 B)
B) 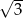 C)
C) 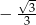 D)
D) 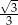
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 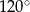 B)
B) 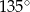 C)
C) 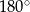 D)
D) 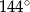
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 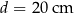 , wysokości
, wysokości 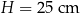 i tworzącej
i tworzącej 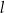 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 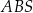 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 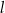 i środku
i środku 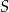 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 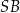 z odcinkiem
z odcinkiem 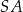 .
.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do 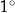 )
)
A) 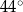 B)
B) 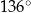 C)
C) 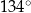 D)
D) 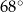
Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 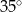 . Miara kąta rozwarcia stożka jest równa
. Miara kąta rozwarcia stożka jest równa
A) 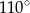 B)
B) 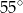 C)
C) 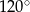 D)
D) 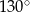
Pole powierzchni bocznej stożka jest dwa razy większe od jego pola podstawy. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem
A) 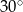 B)
B) 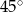 C)
C) 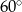 D)
D) 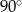
Stożek o promieniu podstawy  i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 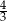 B) 12 C)
B) 12 C) 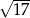 D) 4
D) 4
Stożek o średnicy podstawy 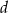 i kula o promieniu
i kula o promieniu 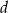 mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 32 B)  C)
C) 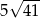 D) 4
D) 4
Jeśli średnica podstawy stożka jest równa 12, a wysokość stożka 8, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 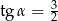 B)
B) 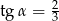 C)
C) 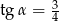 D)
D) 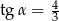
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 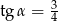 B)
B) 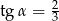 C)
C) 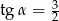 D)
D) 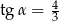
Jeśli średnica podstawy stożka jest równa 16, a wysokość stożka 6, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 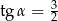 B)
B) 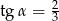 C)
C) 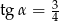 D)
D) 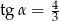
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni bocznej. Wówczas kąt  rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek
A) 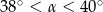 B)
B) 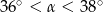 C)
C) 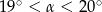 D)
D)