W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 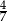 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 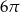 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi ścianami bocznymi ostrosłupa.
między sąsiednimi ścianami bocznymi ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Kąty
W ostrosłupie prawidłowym czworokątnym cosinus kąta między krawędziami bocznymi, które nie są sąsiednie jest równy 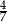 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 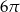 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi krawędziami bocznymi ostrosłupa.
między sąsiednimi krawędziami bocznymi ostrosłupa.
W ostrosłupie prawidłowym czworokątnym krawędź boczna tworzy z krawędzią podstawy kąta  . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy  . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 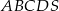 o podstawie
o podstawie 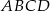 i wierzchołku
i wierzchołku 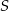 trójkąt
trójkąt 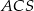 jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).
jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).
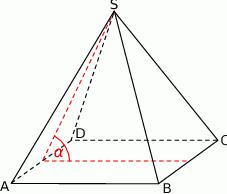
Kąt  jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli
jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli 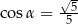 .
.
Dany jest ostrosłup prawidłowy czworokątny o wysokości 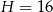 . Suma długości wszystkich jego krawędzi jest równa
. Suma długości wszystkich jego krawędzi jest równa 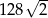 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest sześcian 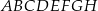 o krawędzi długości 9. Wierzchołki podstawy
o krawędzi długości 9. Wierzchołki podstawy 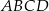 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 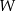 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
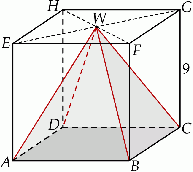
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest graniastosłup prawidłowy czworokątny  o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy
o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy 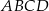 graniastosłupa połączono odcinkami z punktem
graniastosłupa połączono odcinkami z punktem 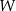 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 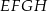 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny 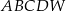 .
.
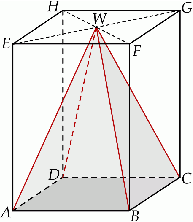
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest ostrosłup prawidłowy czworokątny 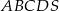 o podstawie
o podstawie 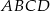 . Ramię trójkąta równoramiennego
. Ramię trójkąta równoramiennego 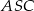 ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
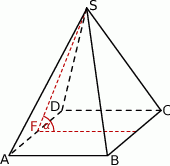
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny, w którym wszystkie krawędzie mają równą długość. Zaznacz na rysunku kąt utworzony przez dwie sąsiednie ściany boczne tego ostrosłupa i oblicz cosinus tego kąta.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt  jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta
jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta  .
.
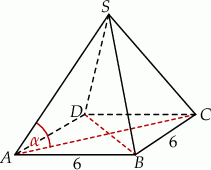
Objętość ostrosłupa prawidłowego czworokątnego  o podstawie
o podstawie 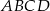 jest równa 224, a promień okręgu opisanego na podstawie
jest równa 224, a promień okręgu opisanego na podstawie 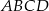 jest równy
jest równy 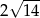 . Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
. Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
Dany jest ostrosłup prawidłowy czworokątny 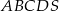 o podstawie
o podstawie 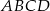 . W trójkącie równoramiennym
. W trójkącie równoramiennym 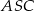 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 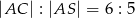 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 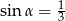 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

