Podstawą ostrosłupa prawidłowego 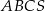 jest trójkąt równoboczny
jest trójkąt równoboczny 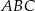 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 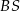 i
i 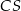 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 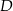 i
i 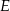 , takie że
, takie że 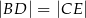 oraz
oraz 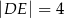 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 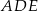 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 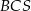 ostrosłupa.
ostrosłupa.
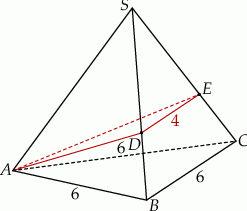
Oblicz objętość tego ostrosłupa.

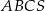 jest trójkąt równoboczny
jest trójkąt równoboczny 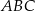 o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych 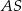 i
i 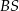 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 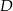 i
i 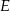 , takie że
, takie że 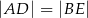 oraz
oraz 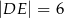 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 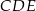 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 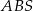 ostrosłupa.
ostrosłupa. 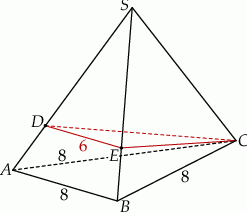
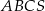 płaszczyzną przechodzącą przez wierzchołek
płaszczyzną przechodzącą przez wierzchołek 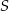 i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość
i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 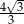 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 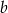 i tworzy z krawędzią podstawy kąt o mierze
i tworzy z krawędzią podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup? 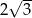 . Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem
. Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem 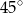 .
.  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 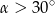 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa. 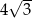 i tworzy z krawędzią boczną kąt
i tworzy z krawędzią boczną kąt  taki, że
taki, że 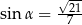 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 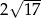 , a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa. 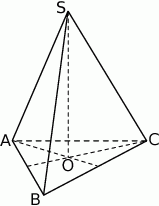
 . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa
. Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 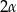 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa. 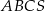 o podstawie
o podstawie 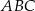 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 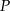 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 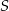 ma miarę
ma miarę 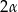 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 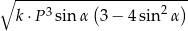 , gdzie
, gdzie 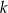 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 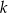 .
. 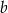 i tworzy z płaszczyzną podstawy kąt o mierze
i tworzy z płaszczyzną podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup? 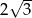 . Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę
. Oblicz objętość tego ostrosłupa jeżeli kąt nachylenia krawędzi bocznej do podstawy ma miarę 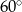 .
. 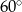 .
. 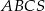 o podstawie
o podstawie 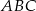 wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 3, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 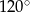 . Oblicz objętość tego ostrosłupa.
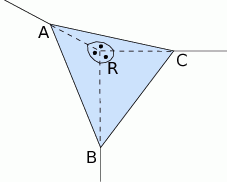
. Oblicz objętość tego ostrosłupa. 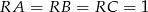 m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01
m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01 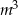 .
. 
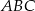 jest podstawą prawidłowego ostrosłupa
jest podstawą prawidłowego ostrosłupa 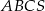 , którego krawędź boczna ma długość 10. Punkt
, którego krawędź boczna ma długość 10. Punkt 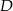 jest środkiem wysokości
jest środkiem wysokości 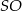 ostrosłupa oraz
ostrosłupa oraz 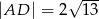 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 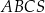 jest równa
jest równa 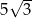 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
(zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 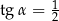 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 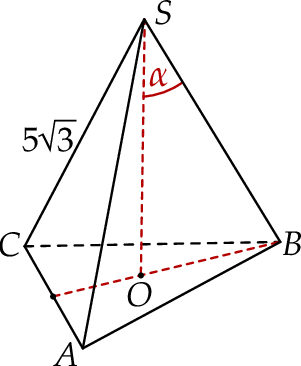
 i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 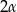 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 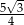 , a pole powierzchni bocznej tego ostrosłupa jest równe
, a pole powierzchni bocznej tego ostrosłupa jest równe 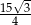 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 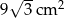 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 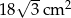 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 