Długości wektorów 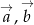 wynoszą odpowiednio 3 i 5. Ponadto znamy ich iloczyn skalarny
wynoszą odpowiednio 3 i 5. Ponadto znamy ich iloczyn skalarny 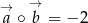 . Obliczyć iloczyn skalarny wektorów
. Obliczyć iloczyn skalarny wektorów 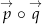 , gdzie
, gdzie 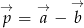 ,
,  .
.
/Szkoła średnia/Geometria/Geometria analityczna/Wektory/Inne
Znajdź punkt dzielący wektor 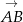 o końcach
o końcach 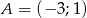 ,
, 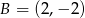 w stosunku -4.
w stosunku -4.
Znajdź wektor jednostkowy, równoległy do wektora ![→ u = [3;− 4]](https://img.zadania.info/zad/4864335/HzadT0x.gif) .
.
Punkty 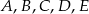 są kolejnymi wierzchołkami pięciokąta, w którym
są kolejnymi wierzchołkami pięciokąta, w którym ![→ → → → AB = [2 ,−3 ], AC = [6,− 2], ED = [3,− 1],CD = [0,4]](https://img.zadania.info/zad/6753416/HzadT1x.gif) . Znajdź współrzędne wektorów
. Znajdź współrzędne wektorów 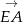 i
i 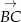 .
.
Wykaż, że dla dowolnych punktów płaszczyzny 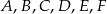 spełniona jest równość.
spełniona jest równość.
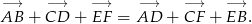
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/9899559/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/9899559/HzadT1x.gif) . Oblicz
. Oblicz 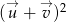 .
.
Ukryj
Podobne zadania
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/2354795/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/2354795/HzadT1x.gif) . Oblicz
. Oblicz 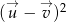 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/7943696/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/7943696/HzadT1x.gif) . Oblicz
. Oblicz 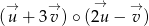 .
.

