Wykres funkcji liniowej 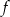 przechodzi przez punkt
przechodzi przez punkt 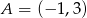 i ma dokładnie jeden punkt wspólny z parabolą o równaniu
i ma dokładnie jeden punkt wspólny z parabolą o równaniu 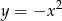 . Znajdź wzór funkcji
. Znajdź wzór funkcji 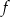 .
.
/Szkoła średnia/Funkcje - wykresy/Liniowy/Wzór z wykresu
Wyznacz wszystkie wartości parametru 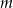 , dla którego funkcja
, dla którego funkcja 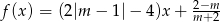 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 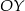 poniżej punktu
poniżej punktu 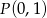 .
.
O funkcji liniowej 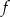 wiadomo, że
wiadomo, że 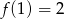 oraz, że do wykresu tej funkcji należy punkt
oraz, że do wykresu tej funkcji należy punkt 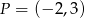 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 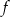 .
.
Dane są funkcje liniowe 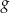 i
i 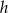 określone wzorami:
określone wzorami: 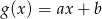 i
i 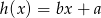 . Wiadomo, że funkcja
. Wiadomo, że funkcja 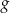 jest rosnąca, a
jest rosnąca, a 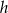 malejąca.
malejąca.
- Wyznacz pierwszą współrzędna punktu przecięcia wykresów tych funkcji.
- Oblicz liczby
 i
i 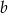 wiedząc, że wykresy funkcji
wiedząc, że wykresy funkcji 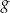 i
i 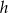 są prostymi prostopadłymi, a punkt ich przecięcia leży na osi
są prostymi prostopadłymi, a punkt ich przecięcia leży na osi 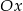 .
.
Wykres funkcji liniowej 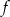 przechodzi przez punkt
przechodzi przez punkt 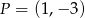 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 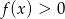 jest przedział
jest przedział 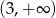 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 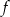 .
.
Wykres funkcji liniowej 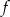 przechodzi przez punkt
przechodzi przez punkt 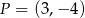 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 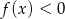 jest przedział
jest przedział 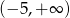 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 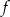 .
.
Wyznacz wzór funkcji 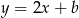 , której wykres ma dokładnie jeden punkt wspólny z wykresem
, której wykres ma dokładnie jeden punkt wspólny z wykresem 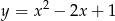 .
.
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkty 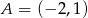 i
i 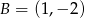 .
.
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkty 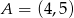 i
i 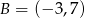 .
.
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkty 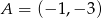 i
i 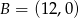 .
.
Prosta o równaniu 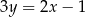 jest osią symetrii wykresu funkcji liniowej
jest osią symetrii wykresu funkcji liniowej 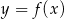 . Ponadto
. Ponadto 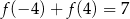 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 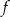 .
.
Dla jakich wartości parametru  istnieje
istnieje 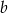 takie, że prosta
takie, że prosta 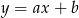 przechodzi przez punkt
przechodzi przez punkt 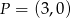 i przecina parabolę
i przecina parabolę 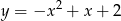 w dwóch punktach o dodatnich odciętych?
w dwóch punktach o dodatnich odciętych?
Wyznacz wzór funkcji liniowej o współczynniku kierunkowym 2 i przechodzącej przez punkt 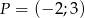 .
.
Wykres funkcji liniowej 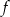 przecina osie
przecina osie  i
i  układu współrzędnych odpowiednio w punktach
układu współrzędnych odpowiednio w punktach 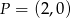 oraz
oraz 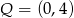 .
.
- Wyznacz wzór funkcji
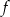 .
. - Sprawdź, czy dla argumentu
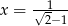 wartość funkcji
wartość funkcji 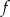 wynosi
wynosi 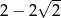 .
.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 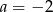 , której wykres przecina oś
, której wykres przecina oś 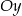 w punkcie
w punkcie 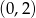 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 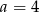 , której wykres przecina oś
, której wykres przecina oś 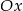 w punkcie
w punkcie 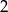 . Wyznacz punkt przecięcia wykresu z osią
. Wyznacz punkt przecięcia wykresu z osią 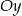 .
.
Napisz wzór funkcji liniowej, której wykres jest równoległy do wykresu funkcji 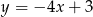 i przecina oś
i przecina oś 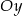 w punkcie
w punkcie 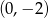 .
.
Wyznacz wzór funkcji liniowej, wiedząc że jej wykres jest nachylony do osi 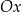 pod kątem
pod kątem 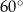 i przechodzi przez punkt
i przechodzi przez punkt 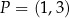 .
.
Wyznacz wzór funkcji liniowej, której wykres tworzy z osią 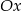 kąt
kąt 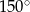 i przechodzi przez punkt
i przechodzi przez punkt 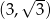 .
.

