Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Ciągi/Geometryczny/W geometrii

Wyszukiwanie zadań

Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.

Długości boków trójkąta 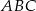ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie 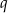q . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 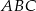ABC są równe miarom kątów trójkąta ABC .

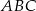O trapezie 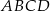ABCD wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków 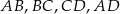AB ,BC ,CD ,AD – w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez 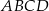ABCD jest rombem.

Wymiary prostopadłościanu o objętości 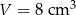3 V = 8 cm i polu powierzchni całkowitej 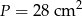P = 28 cm 2 tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.

Ukryj Podobne zadania

Długości trzech krawędzi prostopadłościanu tworzą ciąg geometryczny. Objętość bryły jest równa 27, a suma długości jej krawędzi jest równa 52. Znajdź długość najkrótszej krawędzi prostopadłościanu.

Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy.

W trójkącie prostokątnym długości wysokości i środkowej poprowadzonej z wierzchołka kąta prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, w którym iloczyn wyrazów jest równy 8. Oblicz promień okręgu wpisanego w ten trójkąt.

Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny, w którym największy wyraz jest o 5 większy od wyrazu najmniejszego. Objętość prostopadłościanu jest równa 216. Oblicz długości krawędzi tego prostopadłościanu.

Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.

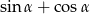Sinus pewnego kąta ostrego α , liczba 2 3 oraz cosinus tego samego kąta α tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę sin α + cos α .

Długości boków trójkąta prostokątnego są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego. Oblicz iloraz tego ciągu.

Długości boków 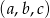(a ,b ,c) trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości 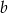b ma miarę 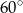60∘ . Oblicz miary pozostałych kątów tego trójkąta.

W graniastosłupie prawidłowym trójkątnym wysokość podstawy, krawędź podstawy i wysokość graniastosłupa tworzą ciąg geometryczny. Oblicz długość krawędzi podstawy graniastosłupa wiedząc, że jego objętość jest równa 108.

Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?

Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 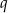q , a cosinus jednego z jego kątów jest równy q − 4 .

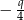  • Wyznacz q .
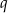  • Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość 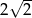√ -- 2 2 , oblicz pole tego trójkąta.