Rozpatrujemy wszystkie stożki, w których suma sześcianów długości promienia podstawy i wysokości jest równa 12. Wyznacz ten spośród rozpatrywanych stożków, którego objętość jest największa. Oblicz tę objętość.
/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największa objętość
W stożek, którego wysokość ma długość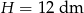 
, a promień jego podstawy ma długość 
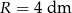wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka jest równa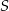 
. Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości 
. Wymiary szkieletu zaznaczono na rysunku.
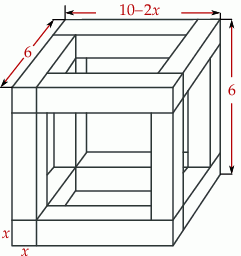
- Wyznacz objętość
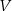drewna potrzebnego do budowy szkieletu jako funkcję zmiennej 
. - Wyznacz dziedzinę funkcji
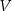. - Oblicz tę wartość
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja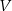 
osiąga wartość największą. Oblicz tę największą objętość.
Ukryj
Podobne zadania
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości 
. Wymiary szkieletu zaznaczono na rysunku.
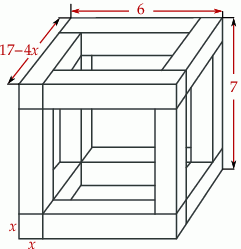
- Wyznacz objętość
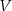drewna potrzebnego do budowy szkieletu jako funkcję zmiennej 
. - Wyznacz dziedzinę funkcji
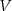. - Oblicz tę wartość
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja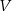 
osiąga wartość największą. Oblicz tę największą objętość.
Podstawą ostrosłupa jest trójkąt prostokątny, w którym tangens jednego z kątów ostrych jest równy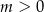 
. Wszystkie krawędzie boczne ostrosłupa mają długość 
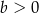. Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe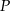 
. Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe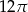 
. Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
Ukryj
Podobne zadania
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe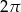 
. Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
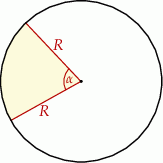
Z papierowego koła o promieniu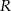 
wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego 
wyciętego wycinka? Wynik podaj w radianach.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe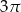 
. Oblicz promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
W kulę o promieniu długości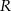 
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
Ukryj
Podobne zadania
W kulę o promieniu długości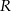 
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
Spośród tych graniastosłupów prawidłowych trójkątnych, których suma długości wszystkich krawędzi jest równa 18, wybierz graniastosłup o największej objętości. Oblicz tę maksymalną objętość.
Ukryj
Podobne zadania
Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?
