Zbieramy z Olkiem znaczki i wczoraj Olek mi powiedział, że ma już 155 znaczków angielskich, francuskich i hiszpańskich. Francuskich ma 2 razy więcej niż hiszpańskich, a angielskich o 39 mniej niż francuskich i hiszpańskich razem. To jednak niemożliwe, uzasadnij dlaczego Olek musiał się pomylić.
/Szkoła podstawowa/Zadania z treścią/Różne
Janek miał łącznie 84 piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich są – odpowiednio – kolejnymi liczbami podzielnymi przez 7. Janek rozdzielił wszystkie piłeczki na siedem identycznych zestawów, przy czym w każdym z nich znalazły się piłeczki w trzech kolorach. Oblicz, ile piłeczek czerwonych, ile – zielonych, a ile – niebieskich było w jednym zestawie.
Ukryj
Podobne zadania
Marta miała łącznie 90 piłeczek, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich są – odpowiednio – kolejnymi liczbami podzielnymi przez 6. Marta rozdzieliła wszystkie piłeczki na sześć identycznych zestawów, przy czym w każdym z nich znalazły się piłeczki w trzech kolorach. Oblicz, ile piłeczek czerwonych, ile – zielonych, a ile – niebieskich było w jednym zestawie.
W kasie są banknoty 10–złotowe, 20–złotowe i 50–złotowe. Liczba banknotów 10–złotowych jest taka sama jak liczba banknotów 50–złotowych i o 32% mniejsza od liczby banknotów 20–złotowych. Łączna wartość wszystkich banknotów 10 i 20–złotowych jest o 540 złotych mniejsza od łącznej wartości wszystkich banknotów 50–złotowych. Oblicz, ile jest wszystkich banknotów w kasie.
Wojtek miał 30 monet dwuzłotowych i 48 monet pięciozłotowych. Połowę monet pięciozłotowych wymienił na monety dwuzłotowe. Kwota z wymiany monet pięciozłotowych stanowiła równowartość kwoty, którą otrzymał w monetach dwuzłotowych. Oblicz, ile łącznie monet dwuzłotowych ma teraz Wojtek.
Jednakowe kubki sprzedawane są w dwóch rodzajach opakowań – małych i dużych. W małym opakowaniu jest dwa razy mniej kubków niż w dużym. W dwóch dużych opakowaniach i sześciu małych znajduje się łącznie 140 kubków. Oblicz, ile kubków jest w sześciu dużych opakowaniach.
Lena posiada pewną liczbę banknotów dwudziestozłotowych i pewną liczbę banknotów dziesięciozłotowych. W sumie banknoty te składają się na kwotę 620 zł. Gdyby połowę banknotów dziesięciozłotowych zamienić na banknoty dwudziestozłotowe, to łączna wartość banknotów wzrosłaby do 750 zł. Ile banknotów dziesięciozłotowych i ile banknotów dwudziestozłotowych posiada Lena? Zapisz obliczenia.
Asia ma w skarbonce 82 zł. Najwięcej w skarbonce jest złotówek, dwa razy więcej niż dwuzłotówek, a cztery razy więcej niż pięciozłotówek. Pozostałe monety w skarbonce to pięćdziesięciogroszówki, których liczba stanowi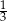 
liczby złotówek. Ile było złotówek w skarbonce?
Wyobraź sobie, że układasz rzędami guziki żółte (ż) i białe (b) według reguły przedstawionej na schemacie:
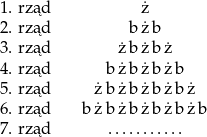
W kolejnym rzędzie najpierw układasz guziki tak, jak w poprzednim rzędzie, a potem dokładasz na obu końcach po jednym guziku, dbając o to, by sąsiednie guziki w rzędzie różniły się kolorami.
Uzupełnij zdania.
A) W 6. rzędzie jest . . . . . . guzików, w tym . . . . . . białych i . . . . . . żółtych.
B) W 7. rzędzie będzie . . . . . . guzików, w tym . . . . . . białych i . . . . . . żółtych.
C) W 100. rzędzie będzie . . . . . . białych i . . . . . . żółtych guzików.
D) W 101. rzędzie będzie . . . . . . białych i . . . . . . żółtych guzików.
E) Jeśli 
jest liczbą parzystą, to w rzędzie o numerze 
będzie . . . . . . białych i . . . . . . żółtych guzików.
Do sklepu rowerowego dostarczono 30 rowerów dziecięcych, wśród których były dwa rodzaje rowerów: dwukołowe i trójkołowe. W sumie w dostarczonych rowerach było 67 kół. Ile rowerów dwukołowych i ile rowerów trójkołowych dostarczono do sklepu? Zapisz obliczenia.
Drwal miał ułożyć 46 okrągłych bali w stosy po 6 bali. Ile takich stosów (patrz rysunek) może ułożyć drwal?
Zapisz obliczenia i odpowiedź.
Na rysunku przedstawiono układ miejsc w przedziale ośmioosobowym wagonu kolejowego i zaznaczono kierunek jazdy pociągu.
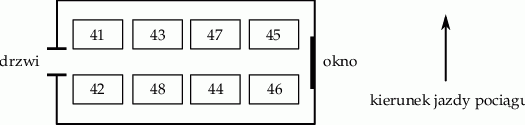
Edyta z Agnieszką planują zakup biletów na wspólną podróż. Wszystkie miejsca w przedziale są wolne. Edyta chce siedzieć przy oknie, natomiast Agnieszka chce siedzieć przodem do kierunku jazdy. Podaj wszystkie możliwości wyboru miejsc spełniające jednocześnie powyższe warunki.
Ukryj
Podobne zadania
Na rysunku przedstawiono układ miejsc w przedziale sześcioosobowym wagonu kolejowego i zaznaczono kierunek jazdy pociągu.
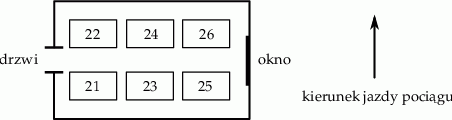
Krzysiek i Antek planują zakup biletów na wspólną podróż. Wszystkie miejsca w przedziale są wolne. Krzysiek chce siedzieć przodem do kierunku jazdy, natomiast Antek chce siedzieć przy oknie lub przy drzwiach, ale nie chce siedzieć naprzeciwko Krzyśka. Podaj wszystkie możliwości wyboru miejsc spełniające jednocześnie powyższe warunki.
Najmniejszym ssakiem na Ziemi jest ryjówka etruska. Najmniejszy zbadany osobnik ważył 2 g. Jego ogon miał 2,5 cm długości i stanowił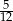 
długości całego ciała. Jaką długość miało ciało ryjówki?
Asi zerwał się naszyjnik. Trzecią część liczby korali znalazła na podłodze, jedną czwartą w kieszeni, jedną piątą pod oparciem kanapy, a szósta część liczby korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku.
W torebce jest mniej niż 100 cukierków. Ile ich jest jeżeli wiadomo, że można je podzielić na 5 równych części, można je podzielić też na 6 równych części, natomiast gdyby je podzielić na 7 części, to w jednej z nich będzie o 3 cukierki mniej od każdej z pozostałych.
W trzech sadach wiśniowych rosła pewna liczba drzew. W pierwszym sadzie znajdowało się 
, a w drugim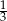 
wszystkich drzew. W trzecim rosło 320 drzew. Ile drzew rosło w każdym sadzie?
Rower dziecięcy ma koło o polu 9 razy mniejszym niż rower kolarski. Ile razy więcej musi obrócić się koło roweru dziecięcego od koła roweru kolarskiego na tej samej drodze?
Ojciec podzielił w testamencie swój majątek pomiędzy trzech synów w ten sposób, że najstarszy miał dostać dwa razy więcej majątku niż średni, zaś średni - dwa razy więcej niż najmłodszy syn. Jaką część majątku otrzymał najmłodszy syn?
W pudełku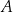 
znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku 
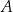były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika 
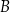, a wszystkie piłeczki, które pozostały w pojemniku 
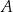przełożono do pojemnika 
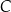. Następnie, wszystkie piłeczki z pojemnika 
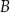podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika 
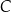podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku 
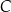jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka 
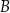. Ile piłeczek czerwonych było początkowo w pudełku 
?
Ela i Ania dostały w prezencie po jednym zestawie puzzli o takiej samej liczbie elementów. Ela ułożyła 
swoich puzzli, a Ania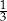 
swoich. Dziewczynki ułożyły łącznie 440 elementów. Oblicz, z ilu elementów składa się jeden zestaw puzzli.
Janek ma 39 znaczków pocztowych w jednej kopercie i 16 w drugiej i chce dołożyć do każdej koperty tyle samo znaczków w tym celu, żeby w pierwszej było 2 razy więcej znaczków niż w drugiej. Po ile znaczków powinien dołożyć do każdej koperty?
