W pudełku znajduje się 420 cukierków w trzech kolorach. Cukierków zielonych jest czterokrotnie więcej niż czerwonych, a cukierków żółtych jest trzy razy mniej niż zielonych i czerwonych razem. Ile cukierków czerwonych należy dołożyć do pudełka, aby stanowiły one 40% cukierków w pudełku?
/Szkoła podstawowa/Zadania z treścią/Różne
Do księgarni językowej dostarczono łącznie 240 książek napisanych w czterech różnych językach. Książek w języku włoskim było 3 razy mniej niż książek w języku niemieckim, książek w języku angielskim było 2 razy więcej niż w języku niemieckim, a książek w języku francuskim było o 20 więcej niż w języku włoskim. Oblicz, ile książek napisanych w języku francuskim dostarczono do tej księgarni.
Kasia przygotowując się do egzaminu rozwiązywała zadania w ciągu 3 dni. Pierwszego dnia rozwiązała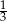 
zadań i jeszcze 4 zadania. Drugiego dnia połowę pozostałych i jeszcze 3 zadania. Trzeciego dnia pozostałych 17 zadań. Ile zadań rozwiązała w ciągu 3 dni?
Chłopiec ma monety po 50 gr i po 20 gr, razem 27 sztuk. Monety mają łączną wartość 8,70 zł. Ile monet po 50 gr, a ile po 20 gr ma chłopiec?
Ukryj
Podobne zadania
Asia wrzucała do skarbonki monety dwu i pięciozłotowe. Po przeliczeniu zawartości skarbonki okazało się, że w skarbonce znajdowało się 395 monet, a uzbierana kwota wynosi 1195 złotych. Oblicz ile monet każdego rodzaju było w skarbonce.
Rozmieniono 34 złote na 116 monet, wśród których były tylko monety 50 i 20 groszowe. Ile było monet 50 groszowych?
W zamkowych podziemiach znajdują się dwie skrzynie otwierane różnymi kluczami. Masz pęk składający się z 6 kluczy, wśród których znajdują się dwa właściwe. Ile co najwyżej prób należy wykonać, aby mieć pewność że dobraliśmy właściwe klucze do skrzyń?
Ania i Jarek grali w kamienie. Na początku gry kamienie układa się w dwóch stosach. Następnie gracze wykonują ruchy na przemian. Ruch w grze polega na wzięciu dowolnej liczby kamieni tylko z jednego ze stosów. Przegrywa ten, kto nie może już wykonać ruchu. Na pewnym etapie gry pierwszy stos zmalał do jednego kamienia, a na drugim znajdowały się trzy kamienie. Ruch miała wykonać Ania. Uzasadnij, że aby zagwarantować sobie wygraną, Ania musiała wziąć dwa kamienie z drugiego stosu.
W pojemniku znajduje się 215 kolorowych plastikowych klocków o jednakowym kształcie. Wśród tych klocków jest 49 klocków czerwonych, 25 niebieskich, 39 żółtych. Pozostałe klocki są zielone. Kacper, nie zaglądając do pudełka, wyjmuje z niego kolejno po jednym klocku. Ile co najmniej klocków musi wyjąć Kacper, żeby mieć pewność, że wśród wyjętych klocków są co najmniej po dwa klocki w każdym z kolorów.
Ukryj
Podobne zadania
W pojemniku znajduje się 60 kolorowych klocków o jednakowym kształcie. Wśród tych klocków jest 25 klocków czerwonych i 17 niebieskich. Pozostałe klocki są zielone. Ania, nie zaglądając do pudełka, wyjmuje z niego kolejno po jednym klocku. Ile co najmniej klocków musi wyjąć Ania, żeby mieć pewność, że wśród wyjętych klocków są co najmniej 3 niebieskie?
W domu kultury zorganizowano konkurs recytatorski. Dla uczestników kupiono nagrody: książki i e-booki. Książki stanowiły 
liczby kupionych nagród. E-booków było o 8 mniej niż książek. Ile kupiono książek?
Ukryj
Podobne zadania
W składzie pewnego pociągu ekspresowego wagony pierwszej klasy stanowią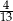 
łącznej liczby wagonów pierwszej i drugiej klasy. W tym samym pociągu jest o 10 wagonów drugiej klasy więcej, niż jest wagonów pierwszej klasy. Ile łącznie wagonów pierwszej i drugiej klasy jest w tym pociągu?
W kasie są banknoty 20–złotowe i 50–złotowe. Liczba banknotów 20–złotowych jest taka sama jak liczba banknotów 50–złotowych. Łączna wartość wszystkich banknotów 50–złotowych jest o 6 tysięcy złotych większa od łącznej wartości wszystkich banknotów 20–złotowych. Oblicz, ile banknotów 20–złotowych jest w kasie.
Ukryj
Podobne zadania
W kasie są banknoty 20–złotowe i 50–złotowe. Liczba banknotów 20–złotowych jest dwa razy większa od liczby banknotów 50–złotowych. Łączna wartość wszystkich banknotów 50–złotowych jest o 3 tysiące złotych większa od łącznej wartości wszystkich banknotów 20–złotowych. Oblicz, ile banknotów 20–złotowych jest w kasie.
Do wykonania naszyjnika Hania przygotowała 4 korale srebrne, 8 korali czerwonych i kilka korali zielonych. Następnie ze wszystkich przygotowanych korali zrobiła naszyjnik. Zielone korale stanowią 20% wszystkich korali w zrobionym naszyjniku. Oblicz, ile zielonych korali jest w naszyjniku.
Ukryj
Podobne zadania
Do wykonania wyszywanego dekoltu z guzikami użyto 7 guzików perłowych, 8 guzików srebrnych i kilku guzików złotych. Złote guziki stanowią 25% wszystkich guzików w gotowym dekolcie. Oblicz, ile złotych guzików jest w gotowym dekolcie.
Paweł powiedział, że podzieli tabliczkę czekolady w taki sposób, że bratu przypadnie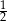 
całej tabliczki, siostrze 
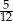całej tabliczki, a jemu 
całej tabliczki. Czy taki podział tabliczki czekolady jest możliwy?
Ukryj
Podobne zadania
Kamil powiedział, że podzieli zgromadzone oszczędności w następujący sposób: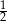 
oszczędności przeznaczy na zakup roweru, 
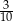oszczędności przeznaczy na zakup deskorolki, 
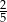oszczędności zachowa na wakacje. Czy taki podział zgromadzonych oszczędności jest możliwy?
Dwie maszyny produkcyjne miały wyprodukować łącznie 10240 plastikowych pojemników. Po zakończeniu produkcji okazało się, że jedna z maszyn przekroczyła plan o 15%, a druga o 20% i w sumie maszyny wyprodukowały 12096 pojemników. Ile pojemników wyprodukowała każda z maszyn?
Puszki z przecierem pomidorowym mają kształt walca o średnicy podstawy 4 cm oraz wysokości 3 cm. Puszki te mogą być na kilka sposobów zapakowane ciasno po 4 sztuki w prostopadłościenne tekturowe pudełka. Wybierz jeden z możliwych sposobów zapakowania puszek, zrób odręczny rysunek siatki odpowiedniego prostopadłościanu i podaj długości krawędzi tego prostopadłościanu.
Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 11, wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.
Ukryj
Podobne zadania
Trzydzieści piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 30, wrzucono do pudełka. Kacper, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Kacper, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą podzielną przez 4? Odpowiedź uzasadnij.
W szufladzie znajduje się 26 różnych par skarpet. Zosia nie zaglądając do szuflady wyjmuje z niej po jednej skarpetce. Ile co najmniej skarpet musi wyjąć Zosia, aby mieć pewność, że wśród wyjętych skarpet są przynajmniej dwie kompletne pary? Odpowiedź uzasadnij.
Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?
Trener chce zamówić 25 nowych piłek do tenisa. Piłki wybranej firmy sprzedawane są w opakowaniach po 3 sztuki albo po 4 sztuki. Ile opakowań każdego rodzaju powinien zamówić trener, aby mieć dokładnie 25 nowych piłek? Podaj wszystkie możliwości.
Ukryj
Podobne zadania
Grupa 29 osób chce się podzielić na kilka grup pięcio i trzyosobowych. Ile grup trzyosobowych może powstać w ten sposób? Podaj wszystkie możliwości.
