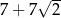W ciągu geometrycznym 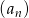 dane są
dane są 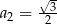 i
i 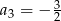 . Wtedy wyraz
. Wtedy wyraz 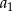 jest równy
jest równy
A) 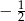 B)
B) 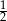 C)
C) 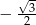 D)
D) 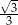
/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny/Dane dwa wyrazy
W ciągu geometrycznym 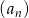 dane są
dane są 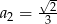 i
i 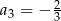 . Wtedy wyraz
. Wtedy wyraz 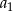 jest równy
jest równy
A) 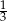 B)
B) 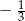 C)
C) 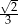 D)
D) 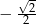
Dany jest ciąg geometryczny 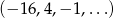 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 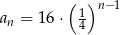 B)
B) 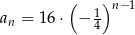 C)
C) 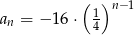 D)
D) 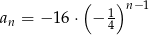
Dany jest ciąg geometryczny 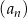 , określony dla
, określony dla 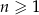 , w którym
, w którym 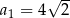 ,
, 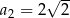 ,
, 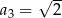 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 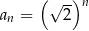 B)
B) 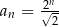 C)
C) 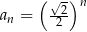 D)
D) 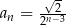
Dany jest ciąg geometryczny 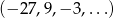 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 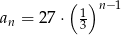 B)
B) 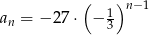 C)
C) 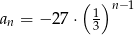 D)
D) 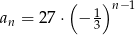
Dany jest ciąg geometryczny 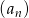 , określony dla
, określony dla 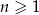 , w którym
, w którym 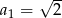 ,
, 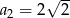 ,
, 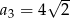 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 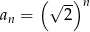 B)
B) 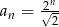 C)
C) 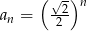 D)
D) 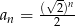
Dany jest ciąg geometryczny 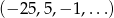 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 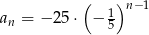 B)
B) 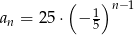 C)
C) 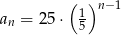 D)
D) 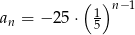
W ciągu geometrycznym drugi wyraz jest równy 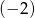 , a trzeci wyraz
, a trzeci wyraz 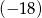 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -9 B) -3 C) 3 D) 9
W ciągu geometrycznym piąty wyraz jest równy  , a szósty wyraz jest równy
, a szósty wyraz jest równy 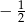 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 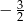 D)
D) 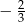
W ciągu geometrycznym drugi wyraz jest równy 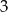 , a trzeci wyraz
, a trzeci wyraz 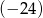 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -8 B) -4 C) 4 D) 8
Ciąg geometryczny 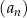 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 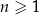 . W tym ciągu
. W tym ciągu 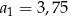 oraz
oraz 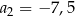 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 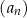 jest równa
jest równa
A) 11,25 B) 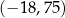 C) 15 D)
C) 15 D) 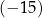
Ciąg geometryczny 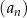 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 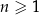 . W tym ciągu
. W tym ciągu 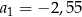 oraz
oraz 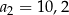 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 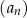 jest równa
jest równa
A) 48,45 B) 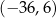 C) 7,65 D)
C) 7,65 D) 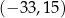
W ciągu geometrycznym 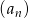 dane są:
dane są: 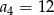 i
i 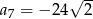 . Ciąg geometryczny
. Ciąg geometryczny 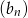 ma taki sam pierwszy wyraz jak ciąg
ma taki sam pierwszy wyraz jak ciąg 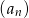 , ale jego iloraz jest dwukrotnością ilorazu ciągu
, ale jego iloraz jest dwukrotnością ilorazu ciągu 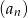 . Zatem
. Zatem
A) 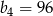 B)
B) 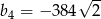 C)
C) 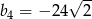 D)
D) 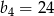
W ciągu geometrycznym 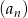 dane są
dane są 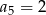 i
i 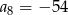 . Wtedy
. Wtedy
A) 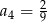 B)
B) 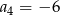 C)
C) 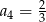 D)
D) 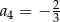
W ciągu geometrycznym 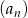 dane są
dane są 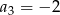 i
i 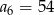 . Wtedy
. Wtedy
A) 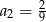 B)
B) 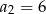 C)
C) 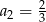 D)
D) 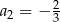
Trzeci wyraz ciągu geometrycznego jest równy 4, a piąty wyraz tego ciągu jest równy 1. Pierwszy wyraz tego ciągu jest równy
A) 4 B) 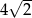 C)
C) 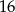 D)
D) 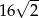
Trzeci wyraz ciągu geometrycznego jest równy 6, a piąty wyraz tego ciągu jest równy 2. Pierwszy wyraz tego ciągu jest równy
A) 18 B) 9 C) 36 D) 12
W rosnącym ciągu geometrycznym 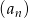 , określonym dla
, określonym dla 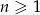 , spełniony jest warunek
, spełniony jest warunek 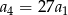 . Iloraz
. Iloraz 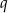 tego ciągu jest równy
tego ciągu jest równy
A) 2 B) 3 C) 4 D) 5
Wszystkie wyrazy ciągu geometrycznego 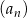 określonego dla
określonego dla 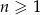 są dodatnie i
są dodatnie i 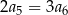 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 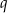 tego ciągu jest równy
tego ciągu jest równy
A) 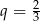 B)
B) 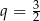 C)
C) 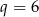 D)
D) 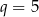
Wszystkie wyrazy ciągu geometrycznego 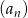 określonego dla
określonego dla 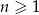 są dodatnie i
są dodatnie i 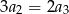 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 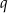 tego ciągu jest równy
tego ciągu jest równy
A) 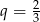 B)
B) 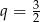 C)
C) 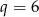 D)
D) 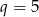
W ciągu geometrycznym 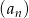 dane są:
dane są: 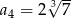 i
i 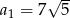 . Wyraz
. Wyraz 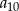 jest równy
jest równy
A) 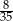 B) 56 C)
B) 56 C) 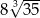 D)
D) 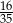
W ciągu geometrycznym rosnącym pierwszy wyraz jest równy 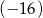 , a siódmy wyraz jest równy
, a siódmy wyraz jest równy 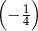 . Kwadrat czwartego wyrazu jest równy
. Kwadrat czwartego wyrazu jest równy
A) 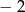 B) 4 C)
B) 4 C) 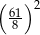 D)
D) 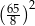
W malejącym ciągu geometrycznym 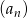 mamy:
mamy: 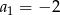 i
i 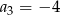 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 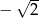 D)
D) 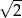
W malejącym ciągu geometrycznym 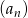 mamy:
mamy: 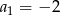 i
i 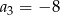 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 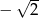 D)
D) 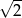
Piąty wyraz rosnącego ciągu geometrycznego jest równy 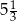 , a siódmy
, a siódmy 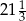 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 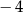 B) 2 C)
B) 2 C) 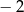 D) 4
D) 4
W malejącym ciągu geometrycznym 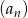 mamy:
mamy: 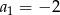 i
i 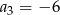 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 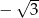 B)
B) 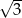 C) -3 D) 3
C) -3 D) 3
Trzeci wyraz malejącego ciągu geometrycznego jest równy 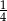 , a piąty
, a piąty 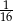 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B) 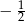 C)
C) 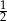 D) 2
D) 2
W rosnącym ciągu geometrycznym 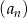 mamy:
mamy: 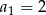 i
i 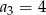 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 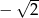 D)
D) 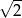
W ciągu geometrycznym 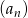 , określonym dla
, określonym dla 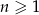 , dane są:
, dane są: 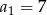 ,
, 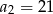 . Wtedy
. Wtedy
A) 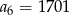 B)
B) 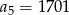 C)
C) 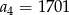 D)
D) 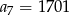
W ciągu geometrycznym 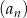 , określonym dla
, określonym dla 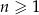 , dane są:
, dane są: 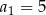 ,
, 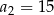 . Wtedy
. Wtedy
A) 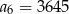 B)
B) 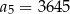 C)
C) 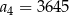 D)
D) 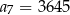
W ciągu geometrycznym 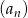 dane są:
dane są: 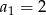 i
i 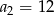 . Wtedy
. Wtedy
A) 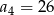 B)
B) 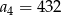 C)
C) 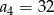 D)
D) 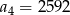
Jeżeli w ciągu geometrycznym 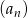 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 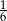 , a drugi wynosi
, a drugi wynosi 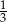 , to
, to
A) 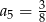 B)
B) 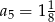 C)
C) 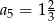 D)
D) 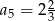
W ciągu geometrycznym 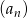 dane są:
dane są: 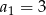 i
i 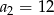 . Wtedy
. Wtedy
A) 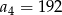 B)
B) 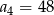 C)
C) 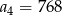 D)
D) 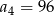
W ciągu geometrycznym 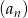 dane są:
dane są: 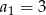 i
i 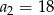 . Wtedy
. Wtedy
A) 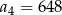 B)
B) 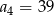 C)
C) 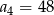 D)
D) 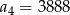
W ciągu geometrycznym 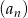 dane są:
dane są: 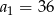 i
i 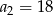 . Wtedy
. Wtedy
A) 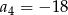 B)
B) 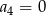 C)
C) 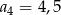 D)
D) 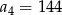
Jeżeli w ciągu geometrycznym 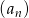 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 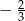 , a drugi wynosi 2, to
, a drugi wynosi 2, to
A) 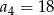 B)
B) 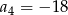 C)
C) 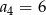 D)
D) 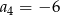
Dany jest ciąg geometryczny 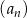 , określony dla
, określony dla 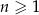 , w którym
, w którym 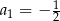 ,
, 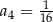 . Suma czterech początkowych wyrazów ciągu
. Suma czterech początkowych wyrazów ciągu 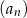 jest równa
jest równa
A) 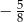 B)
B) 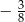 C)
C) 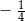 D)
D) 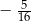
Dany jest ciąg geometryczny 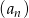 , w którym
, w którym 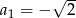 ,
, 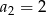 ,
, 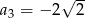 . Dziesiąty wyraz tego ciągu, czyli
. Dziesiąty wyraz tego ciągu, czyli 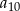 , jest równy
, jest równy
A) 32 B) 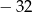 C)
C) 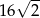 D)
D) 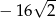
Dany jest ciąg geometryczny 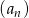 , w którym
, w którym 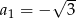 ,
, 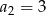 ,
, 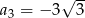 . Dziewiąty wyraz tego ciągu, czyli
. Dziewiąty wyraz tego ciągu, czyli 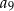 , jest równy
, jest równy
A) 243 B) 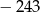 C)
C) 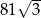 D)
D) 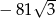
Dany jest ciąg geometryczny 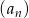 , określony dla
, określony dla 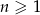 , o którym wiemy, że:
, o którym wiemy, że: 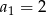 i
i 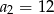 . Wtedy
. Wtedy 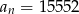 dla
dla
A) 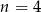 B)
B) 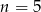 C)
C) 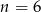 D)
D) 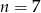
Dany jest ciąg geometryczny 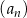 , określony dla
, określony dla 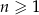 , o którym wiemy, że:
, o którym wiemy, że: 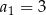 i
i 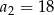 . Wtedy
. Wtedy 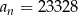 dla
dla
A) 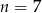 B)
B) 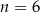 C)
C) 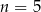 D)
D) 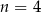
Jaką liczbę można wstawić pomiędzy 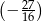 i
i 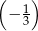 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 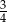 B)
B) 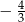 C)
C) 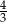 D)
D) 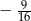
Jaką liczbę można wstawić pomiędzy liczby 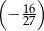 i
i 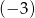 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 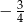 B)
B) 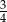 C)
C) 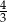 D)
D) 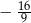
W ciągu geometrycznym rosnącym 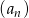 wyraz
wyraz 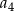 jest równy 4, a wyraz
jest równy 4, a wyraz 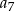 jest równy 32. Wskaż wzór na
jest równy 32. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 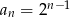 B)
B) 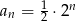 C)
C) 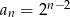 D)
D) 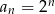
W ciągu geometrycznym rosnącym 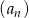 wyraz
wyraz 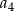 jest równy 6, a wyraz
jest równy 6, a wyraz 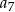 jest równy 48. Wskaż wzór na
jest równy 48. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 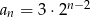 B)
B) 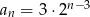 C)
C) 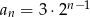 D)
D) 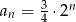
W ciągu geometrycznym rosnącym 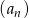 wyraz
wyraz 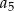 jest równy 4, a wyraz
jest równy 4, a wyraz 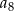 jest równy 32. Wskaż wzór na
jest równy 32. Wskaż wzór na  -ty wyraz ciągu
-ty wyraz ciągu
A) 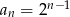 B)
B) 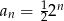 C)
C) 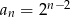 D)
D) 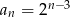
Wzorem ogólnym ciągu geometrycznego w którym 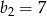 i
i 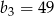 jest:
jest:
A) 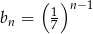 B)
B) 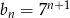 C)
C) 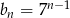 D)
D) 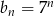
Wzorem ogólnym ciągu geometrycznego w którym 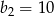 i
i 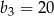 jest:
jest:
A) 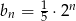 B)
B) 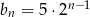 C)
C) 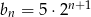 D)
D) 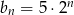
Liczby 2,6 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 162 B) 54 C) 18 D) 9
Liczby 3,12 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 192 B) 96 C) 768 D) 48
Liczby 4,12 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 36 B) 108 C) 48 D) 324
Dany jest ciąg geometryczny 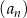 , określony dla
, określony dla 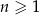 , w którym
, w którym 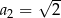 ,
, 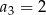 . Suma sześciu początkowych wyrazów ciągu
. Suma sześciu początkowych wyrazów ciągu 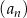 jest równa
jest równa
A) 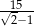 B)
B) 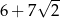 C)
C) 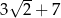 D)
D)