Dany jest ciąg o wyrazie ogólnym 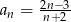 . Wynika stąd, że
. Wynika stąd, że
A) 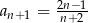 B)
B) 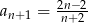 C)
C) 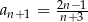 D)
D) 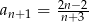
/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Wymierny
Dany jest ciąg o wyrazie ogólnym 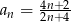 . Wynika stąd, że
. Wynika stąd, że
A) 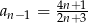 B)
B) 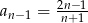 C)
C) 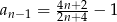 D)
D) 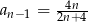
Piąty wyraz ciągu 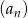 określonego wzorem
określonego wzorem 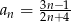 , gdzie
, gdzie 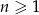 jest równy
jest równy
A) 1 B) 5 C) 10 D) 0,5
Szósty wyraz ciągu 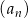 określonego wzorem
określonego wzorem 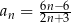 , gdzie
, gdzie 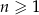 jest równy
jest równy
A) 2 B) 1 C) 12 D) 0,5
Ciąg 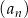 jest określony wzorem
jest określony wzorem 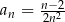 dla każdej liczby naturalnej
dla każdej liczby naturalnej 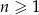 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 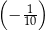 B)
B) 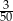 C)
C) 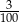 D)
D) 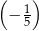
Piąty wyraz ciągu 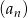 określonego wzorem
określonego wzorem 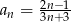 , gdzie
, gdzie 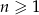 jest równy
jest równy
A) 1 B) 5 C) 10 D) 0,5
Ciąg 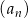 jest określony wzorem
jest określony wzorem 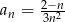 dla każdej liczby naturalnej
dla każdej liczby naturalnej 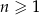 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 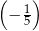 B)
B) 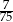 C)
C) 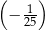 D)
D) 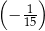
Ciąg 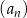 jest określony wzorem
jest określony wzorem 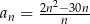 dla każdej liczby naturalnej
dla każdej liczby naturalnej 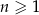 . Wtedy
. Wtedy 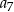 jest równy
jest równy
A) 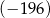 B)
B) 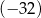 C)
C) 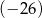 D)
D) 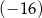
Ciąg 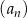 jest określony wzorem
jest określony wzorem 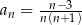 dla każdej liczby naturalnej
dla każdej liczby naturalnej 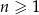 . Wynika stąd, że suma siedmiu początkowych wyrazów ciągu
. Wynika stąd, że suma siedmiu początkowych wyrazów ciągu 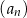 jest większa od sumy pięciu początkowych wyrazów ciągu
jest większa od sumy pięciu początkowych wyrazów ciągu 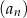 o
o
A)  B)
B) 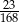 C)
C) 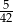 D) 0
D) 0
Ciąg 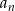 dany jest wzorem
dany jest wzorem 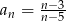 , gdzie
, gdzie 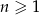 oraz
oraz 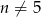 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 1 B) 2 C) 3 D) 4
Ciąg 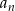 dany jest wzorem
dany jest wzorem 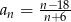 , gdzie
, gdzie 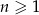 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 2 B) 3 C) 4 D) 6
Ciąg 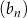 jest określony wzorem
jest określony wzorem 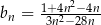 dla każdej liczby naturalnej
dla każdej liczby naturalnej 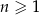 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 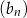 jest równa
jest równa
A) 8 B) 9 C) 13 D) 14
Dany jest ciąg o wyrazie ogólnym 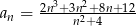 . Suma dwudziestu początkowych wyrazów tego ciągu jest równa
. Suma dwudziestu początkowych wyrazów tego ciągu jest równa
A) 480 B) 380 C) 280 D) 180
Wyraz ogólny ciągu 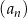 ma postać
ma postać 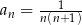 , gdzie
, gdzie 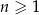 . Wobec tego
. Wobec tego
A) 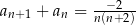 B)
B) 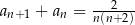
C) 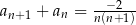 D)
D) 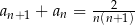
Wyraz ogólny ciągu 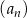 ma postać
ma postać 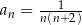 , gdzie
, gdzie 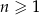 . Wobec tego
. Wobec tego
A) 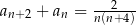 B)
B) 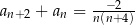
C) 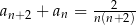 D)
D) 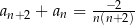
Który wyraz ciągu 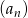 o wyrazie ogólnym
o wyrazie ogólnym 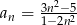 jest równy
jest równy 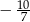 ?
?
A) piąty B) dwudziesty piąty C) siódmy D) dziewiąty
Który wyraz ciągu 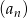 o wyrazie ogólnym
o wyrazie ogólnym 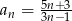 jest równy 2?
jest równy 2?
A) piąty B) siedemnasty C) siódmy D) dziewiąty
Który wyraz ciągu 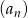 o wyrazie ogólnym
o wyrazie ogólnym 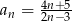 jest równy 3?
jest równy 3?
A) piąty B) siedemnasty C) siódmy D) dziewiąty
Ciąg 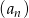 określony jest wzorem
określony jest wzorem 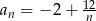 dla
dla 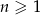 . Równość
. Równość 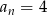 zachodzi dla
zachodzi dla
A) 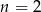 B)
B) 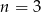 C)
C) 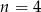 D)
D) 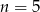
Dany jest ciąg o wzorze ogólnym 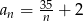 . Wartość
. Wartość  ma wyraz
ma wyraz
A) szesnasty B) trzydziesty pierwszy C) siedemdziesiąty D) osiemnasty
Dany jest ciąg 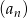 jest określony wzorem
jest określony wzorem 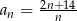 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 5 B) 4 C) 3 D) 2
Dany jest ciąg 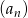 jest określony wzorem
jest określony wzorem 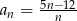 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 6 B) 4 C) 3 D) 7
Ciąg 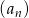 jest określony wzorem
jest określony wzorem 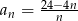 dla
dla 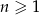 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 7 B) 6 C) 5 D) 4
Dany jest ciąg 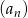 jest określony wzorem
jest określony wzorem 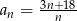 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 5 B) 4 C) 8 D) 6
Ciąg 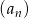 jest określony wzorem
jest określony wzorem 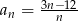 dla
dla 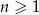 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 6 B) 4 C) 3 D) 2
Dany jest ciąg 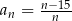 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 0 B) 1 C) 3 D) 4
Dany jest nieskończony ciąg 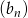 , dla którego
, dla którego 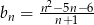 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Dany jest nieskończony ciąg 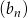 , dla którego
, dla którego 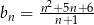 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Dany jest nieskończony ciąg 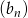 , dla którego
, dla którego 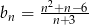 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Ciąg 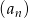 o wyrazie ogólnym
o wyrazie ogólnym 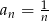 jest ciągiem
jest ciągiem
A) malejącym B) arytmetycznym C) rosnącym D) geometrycznym
Ciąg 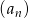 o wyrazie ogólnym
o wyrazie ogólnym 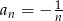 jest ciągiem
jest ciągiem
A) malejącym B) arytmetycznym C) rosnącym D) geometrycznym
Ciąg 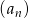 o wyrazie ogólnym
o wyrazie ogólnym 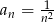 jest ciągiem
jest ciągiem
A) arytmetycznym B) malejącym C) rosnącym D) geometrycznym

