Dany jest trapez 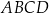 , w którym przekątna
, w którym przekątna 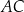 jest prostopadła do ramienia
jest prostopadła do ramienia 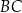 ,
, 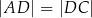 oraz
oraz 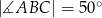 (zobacz rysunek).
(zobacz rysunek).
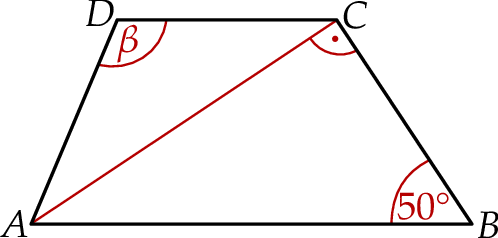
Stąd wynika, że
A) 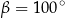 B)
B) 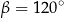 C)
C) 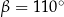 D)
D) 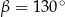
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trapez 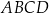 , w którym przekątna
, w którym przekątna 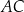 jest prostopadła do ramienia
jest prostopadła do ramienia 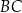 ,
, 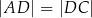 oraz
oraz 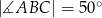 (zobacz rysunek).
(zobacz rysunek).
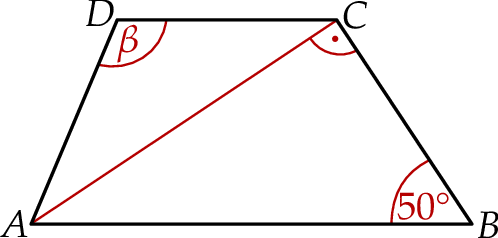
Stąd wynika, że
A) 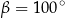 B)
B) 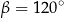 C)
C) 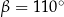 D)
D) 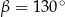
Dany jest trapez 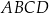 , w którym bok
, w którym bok 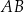 jest równoległy do boku
jest równoległy do boku 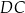 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 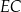 równoległy do boku
równoległy do boku 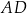 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 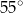 B)
B) 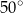 C)
C) 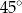 D)
D) 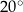
Dany jest trapez 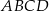 , w którym przekątna
, w którym przekątna 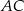 jest prostopadła do ramienia
jest prostopadła do ramienia 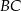 ,
, 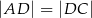 oraz
oraz 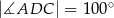 (zobacz rysunek).
(zobacz rysunek).
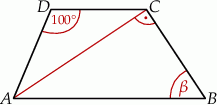
Stąd wynika, że
A) 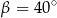 B)
B) 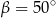 C)
C) 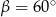 D)
D) 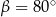
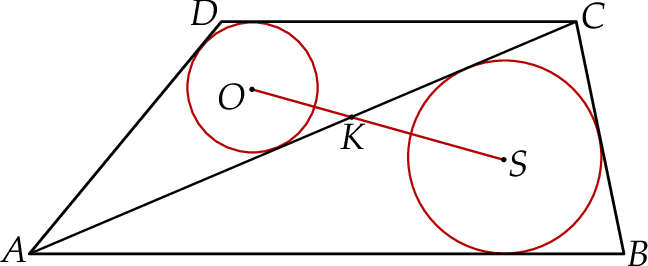
Trapez 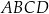 podzielono przekątną
podzielono przekątną 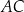 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 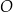 i
i 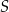 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 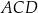 i
i 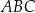 , a odcinek
, a odcinek 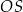 przecina przekątną
przecina przekątną 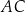 w punkcie
w punkcie 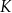 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 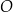 i
i 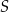 jest równy
jest równy  , a odcinek
, a odcinek 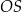 ma długość 24.
ma długość 24.
Wtedy
A) 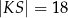 B)
B) 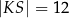 C)
C) 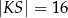 D)
D) 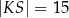
Na rysunku przedstawiono trapez 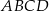 o podstawach
o podstawach 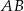 i
i 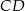 , w którym
, w którym 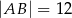 i
i 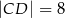 .
.
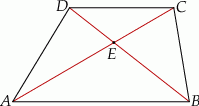
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Pola trójkątów utworzonych przez przekątne trapezu i jego boki spełniają równość
A) 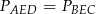 B)
B) 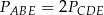 C)
C) 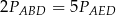
D) 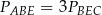 E)
E) 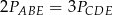 F)
F) 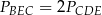
W trapezie miary kątów ostrych są równe 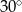 i
i 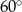 . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A) 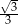 B)
B) 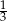 C)
C) 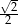 D)
D) 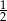
Trapez 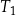 , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu 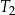 . Pole trapezu
. Pole trapezu 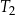 jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 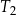 jest równy
jest równy
A) 18 B) 9 C) 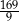 D)
D) 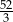
W trapezie 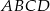 (
(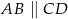 ) dłuższa podstawa ma długość
) dłuższa podstawa ma długość 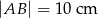 . Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
. Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
A) 5 cm B) 7 cm C) 4 cm D) 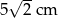
W trapezie 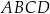 o podstawach
o podstawach 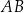 i
i 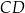 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 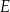 (zobacz rysunek).
(zobacz rysunek).
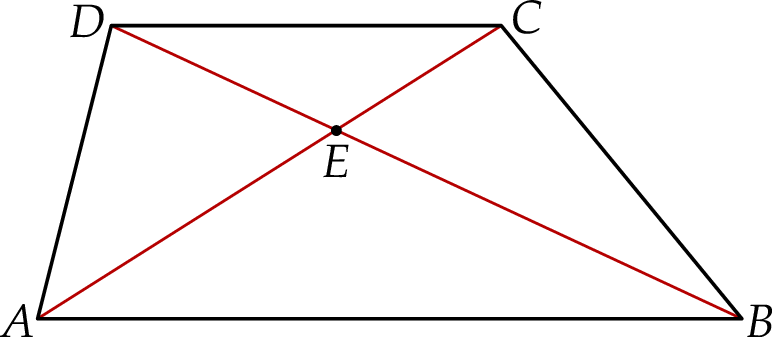
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 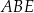 jest podobny do trójkąta jest podobny do trójkąta 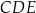 . . | P | F |
Pole trójkąta 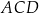 jest równe polu trójkąta jest równe polu trójkąta 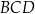 . . | P | F |
W trapezie 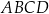 podstawa
podstawa 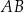 jest dłuższa od podstawy
jest dłuższa od podstawy 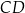 . Przekątne trapezu przecinają się w punkcie
. Przekątne trapezu przecinają się w punkcie 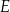 (zobacz rysunek).
(zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 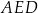 jest równe polu trójkąta jest równe polu trójkąta 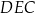 . . | P | F |
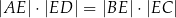 | P | F |
Różnica miar dwóch kątów rozwartych trapezu jest równa 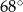 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 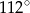 B)
B) 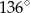 C)
C) 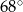 D)
D) 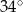
Przekątne trapezu 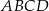 , w którym
, w którym 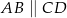 przecinają się w punkcie
przecinają się w punkcie 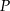 w ten sposób, że
w ten sposób, że 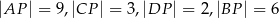 oraz
oraz 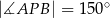 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Dany jest trapez 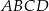 , w którym
, w którym 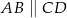 oraz przekątne
oraz przekątne 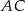 i
i 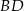 przecinają się w punkcie
przecinają się w punkcie 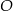 . Wysokość tego trapezu jest równa 12. Obwód trójkąta
. Wysokość tego trapezu jest równa 12. Obwód trójkąta 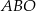 jest równy 39, a obwód trójkąta
jest równy 39, a obwód trójkąta 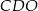 jest równy 13.
jest równy 13.
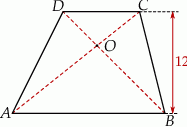
Wysokość trójkąta 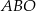 poprowadzona z punktu
poprowadzona z punktu 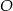 jest równa
jest równa
A) 3 B) 4 C) 9 D) 6
Dany jest trapez 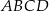 , w którym
, w którym 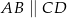 oraz przekątne
oraz przekątne 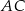 i
i 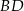 przecinają się w punkcie
przecinają się w punkcie 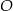 . Wysokość tego trapezu jest równa 15. Obwód trójkąta
. Wysokość tego trapezu jest równa 15. Obwód trójkąta 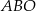 jest równy 42, a obwód trójkąta
jest równy 42, a obwód trójkąta 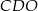 jest równy 14.
jest równy 14.
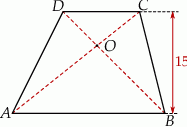
Wysokość trójkąta 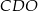 poprowadzona z punktu
poprowadzona z punktu 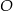 jest równa
jest równa
A) 3,75 B) 5 C) 6 D) 7,5
Długości podstaw trapezu wynoszą  oraz
oraz 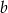 , gdzie
, gdzie 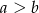 . Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
. Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
A) 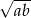 B)
B) 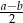 C)
C) 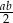 D)
D) 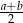
Przekątne trapezu 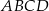 przecinają się w punkcie
przecinają się w punkcie 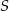 w ten sposób, że pole trójkąta
w ten sposób, że pole trójkąta 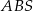 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 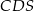 .
.
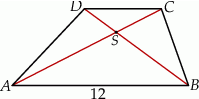
Jeżeli podstawa 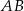 ma długość 12, to długość podstawy
ma długość 12, to długość podstawy 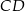 jest równa
jest równa
A) 8 B) 3 C) 6 D) 9
W trapezie 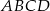 , w którym
, w którym 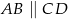 , przedłużono ramiona
, przedłużono ramiona 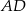 i
i 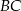 do przecięcia się w punkcie
do przecięcia się w punkcie 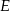 . Wiadomo, że
. Wiadomo, że 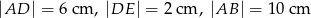 . Wobec tego odcinek
. Wobec tego odcinek 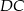 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
W trapezie 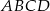 , w którym
, w którym 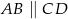 , przedłużono ramiona
, przedłużono ramiona 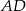 i
i 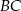 do przecięcia się w punkcie
do przecięcia się w punkcie 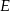 . Wiadomo, że
. Wiadomo, że 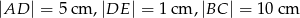 . Wobec tego odcinek
. Wobec tego odcinek 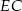 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
W trapezie 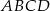 , w którym
, w którym 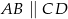 , przedłużono ramiona
, przedłużono ramiona 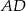 i
i 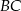 do przecięcia się w punkcie
do przecięcia się w punkcie 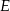 . Wiadomo, że
. Wiadomo, że 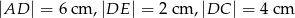 . Wobec tego odcinek
. Wobec tego odcinek 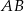 ma długość
ma długość
A) 15,5 cm B) 15 cm C) 16 cm D) 16,5 cm
W trapezie 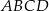 o podstawach
o podstawach 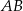 i
i 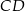 dane są:
dane są: 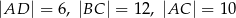 oraz
oraz 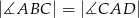 (zobacz rysunek).
(zobacz rysunek).
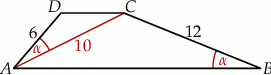
Wówczas długość podstawy 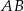 tego trapezu jest równa
tego trapezu jest równa
A) 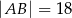 B)
B) 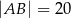 C)
C) 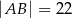 D)
D) 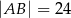
W trapezie 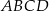 o podstawach
o podstawach 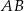 i
i 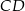 dane są:
dane są: 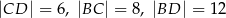 oraz
oraz 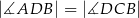 (zobacz rysunek).
(zobacz rysunek).
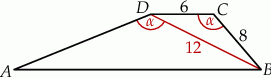
Wówczas długość ramienia 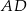 tego trapezu jest równa
tego trapezu jest równa
A) 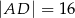 B)
B) 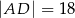 C)
C) 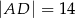 D)
D) 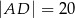
Kąty wewnętrzne przy wierzchołkach 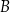 i
i 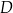 trapezu
trapezu 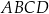 są równe odpowiednio
są równe odpowiednio 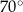 i
i 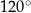 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 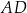 i
i 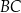 przecinają się pod kątem
przecinają się pod kątem
A) 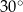 B)
B) 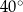 C)
C) 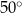 D)
D) 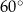
Kąty wewnętrzne przy wierzchołkach 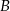 i
i 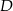 trapezu
trapezu 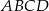 są równe odpowiednio
są równe odpowiednio 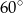 i
i 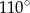 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 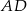 i
i 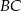 przecinają się pod kątem
przecinają się pod kątem
A) 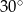 B)
B) 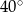 C)
C) 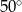 D)
D) 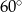
Przekątne trapezu 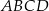 przecinają się w punkcie
przecinają się w punkcie 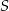 w ten sposób, że
w ten sposób, że 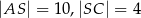 ,
, 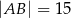 .
.
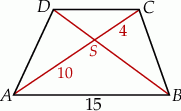
Długość odcinka 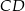 jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
Przekątne trapezu 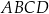 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że
w ten sposób, że 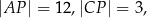
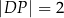 . Długość odcinka
. Długość odcinka 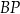 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Przekątne trapezu 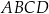 o podstawach
o podstawach 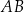 i
i 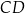 przecinają się w punkcie
przecinają się w punkcie 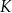 w ten sposób, że
w ten sposób, że 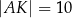 ,
, 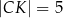 ,
, 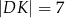 . Długość odcinka
. Długość odcinka 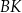 jest równa
jest równa
A) 7 B) 14 C) 10 D) 8
Przekątne trapezu 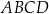 przecinają się w punkcie
przecinają się w punkcie 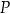 w ten sposób, że
w ten sposób, że 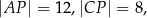
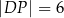 . Długość odcinka
. Długość odcinka 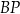 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
