Wykaż, że jeżeli liczby rzeczywiste  i
i 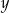 spełniają warunek
spełniają warunek
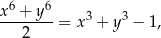
to 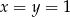 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli liczby rzeczywiste  i
i 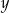 spełniają warunek
spełniają warunek
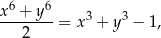
to 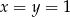 .
.
Wykaż, że jeżeli liczby dodatnie  i
i 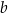 spełniają warunek
spełniają warunek
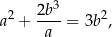
to spełniają też równość
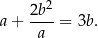
Wykaż, że jeżeli 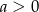 i
i 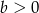 oraz
oraz 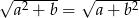 , to
, to 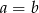 lub
lub 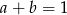 .
.
Wykaż, że jeśli 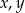 są liczbami różnymi od zera i
są liczbami różnymi od zera i 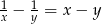 , to
, to 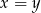 lub
lub 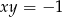 .
.
Wykaż, że jeżeli 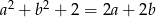 , to
, to 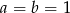 .
.
Udowodnij, że jeżeli 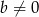 i
i 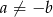 , to
, to 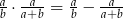 .
.
Uzasadnij, że jeśli 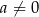 oraz
oraz 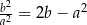 , to
, to 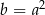 .
.
Uzasadnij, że jeśli 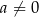 oraz
oraz 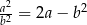 , to
, to 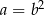 .
.
Wykaż, że jeśli 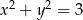 i
i 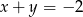 , to
, to 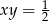 .
.
Wykaż, że jeśli 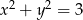 i
i 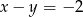 , to
, to 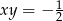 .
.
Suma dwóch liczb jest równa 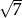 , a ich różnica jest równa
, a ich różnica jest równa 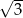 . Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
. Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
Uzasadnij, że jeżeli 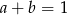 i
i 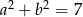 , to
, to 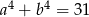 .
.
Uzasadnij, że jeżeli 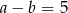 i
i 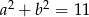 , to
, to 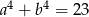 .
.
Wykaż, że jeżeli liczby  i
i 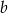 spełniają równość
spełniają równość 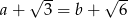 to przynajmniej jedna z nich jest niewymierna.
to przynajmniej jedna z nich jest niewymierna.
Liczby dodatnie  i
i 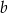 spełniają równość
spełniają równość 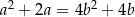 . Wykaż, że
. Wykaż, że 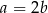 .
.
Liczby dodatnie  i
i 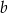 spełniają równość
spełniają równość 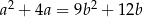 . Wykaż, że
. Wykaż, że 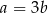 .
.
Wykaż, że dla dowolnych liczb dodatnich  i
i 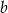 spełniona jest równość
spełniona jest równość
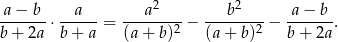
Wykaż, że jeżeli 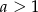 i
i 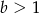 oraz
oraz 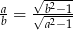 to
to 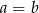 .
.
Wykaż, że jeżeli 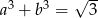 i
i 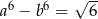 to
to 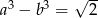 .
.
Liczby rzeczywiste  i
i 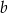 spełniają równość
spełniają równość 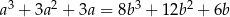 . Wykaż, że
. Wykaż, że 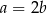 .
.
Uzasadnij, że jeśli 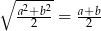 to
to 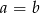 .
.
Wykaż, że jeżeli 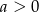 i
i 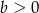 oraz
oraz 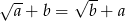 to
to 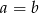 lub
lub 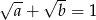 .
.
Wykaż, że jeżeli liczby dodatnie  i
i 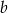 spełniają warunek
spełniają warunek
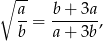
to 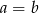 .
.
Wykaż, że jeżeli liczby dodatnie 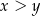 spełniają warunki:
spełniają warunki: 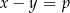 i
i 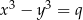 , to
, to
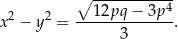
Udowodnij, że jeżeli liczba 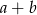 jest różna od zera oraz
jest różna od zera oraz 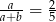 to
to 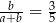 .
.
Suma dwóch liczb jest równa 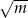 , a ich różnica jest równa
, a ich różnica jest równa 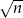 , gdzie
, gdzie 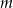 i
i  są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
