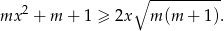Udowodnij, że jeżeli 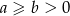 to
to 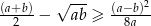 .
.
/Szkoła średnia/Nierówności/Udowodnij.../Z pierwiastkami
Uzasadnij, że jeżeli 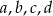 są liczbami dodatnimi to
są liczbami dodatnimi to
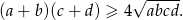
Wykaż, że dla dowolnych różnych liczb rzeczywistych 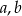 prawdziwa jest nierówność
prawdziwa jest nierówność
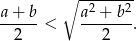
Wykaż, że jeśli 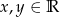 to
to 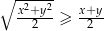 .
.
Uzasadnij, że jeżeli 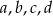 są liczbami dodatnimi to
są liczbami dodatnimi to
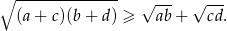
Wykaż, że dla 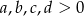 prawdziwa jest nierówność
prawdziwa jest nierówność 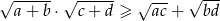 .
.
Udowodnij, że dla dowolnych liczb nieujemnych  i
i 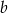 prawdziwa jest nierówność
prawdziwa jest nierówność
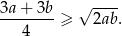
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
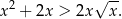
Udowodnij, że dla dowolnych liczb dodatnich  i
i 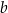 prawdziwa jest nierówność
prawdziwa jest nierówność
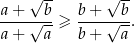
Wykaż, że jeżeli 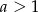 to prawdziwa jest nierówność
to prawdziwa jest nierówność
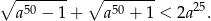
Wykaż, że dla każdej liczby 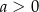 i dla każdej liczby
i dla każdej liczby 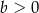 prawdziwa jest nierówność
prawdziwa jest nierówność
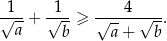
Wykaż, że dla dowolnych liczb rzeczywistych 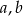 spełniona jest nierówność
spełniona jest nierówność
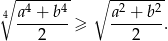
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 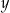 prawdziwa jest nierówność
prawdziwa jest nierówność
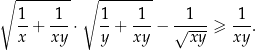
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 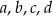 prawdziwa jest nierówność
prawdziwa jest nierówność
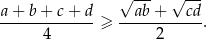
Wykaż, że prawdziwa jest nierówność 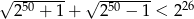 .
.
Wykaż, że dla dowolnych liczb ujemnych 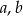 spełniona jest nierówność
spełniona jest nierówność
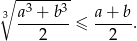
Wykaż, że
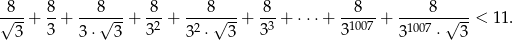
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 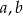 prawdziwa jest nierówność
prawdziwa jest nierówność
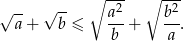
Uzasadnij, że jeśli liczby rzeczywiste 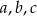 spełniają nierówności
spełniają nierówności 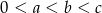 , to
, to
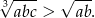
- Wykaż, że dla dowolnych różnych liczb dodatnich
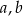 prawdziwa jest nierówność
prawdziwa jest nierówność 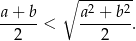
- Wykorzystując nierówność z punktu a), wykaż, że prawdziwa jest nierówność
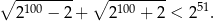
Wykaż, że jeżeli 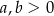 to
to 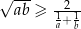 .
.
Wykaż, że jeżeli 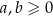 to
to 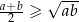 .
.
Wykaż, że jeżeli 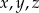 są długościami boków trójkąta to
są długościami boków trójkąta to 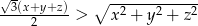 .
.
Udowodnij, że dowolne liczby rzeczywiste  i
i 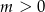 spełniają nierówność
spełniają nierówność