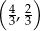W układzie współrzędnych zaznaczono wierzchołki 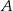 i
i 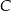 kwadratu
kwadratu 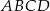 .
.
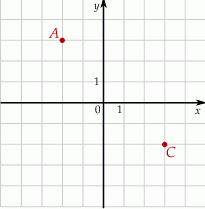
Pole kwadratu 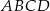 jest równe
jest równe
A) 25 B) 20 C) 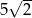 D) 5
D) 5
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W układzie współrzędnych zaznaczono wierzchołki 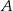 i
i 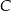 kwadratu
kwadratu 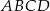 .
.

Pole kwadratu 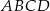 jest równe
jest równe
A) 25 B) 20 C) 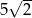 D) 5
D) 5
Końce odcinka 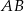 mają współrzędne
mają współrzędne 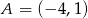 i
i 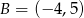 . Na symetralnej odcinka
. Na symetralnej odcinka 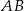 leży punkt o współrzędnych
leży punkt o współrzędnych
A) 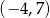 B)
B) 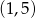 C)
C) 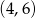 D)
D) 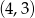
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 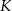 ,
, 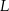 i środku w punkcie
i środku w punkcie 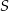 . Punkt
. Punkt 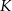 ma współrzędne
ma współrzędne 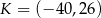 , a punkt
, a punkt 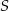 współrzędne
współrzędne 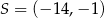 . Na którym rysunku zacieniowana część płaszczyzny zawiera punkt
. Na którym rysunku zacieniowana część płaszczyzny zawiera punkt 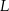 ?
?
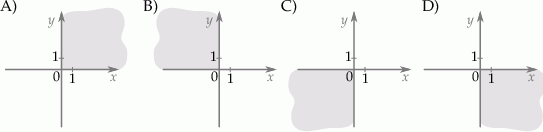
Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.
Obwód narysowanego trójkąta jest równy
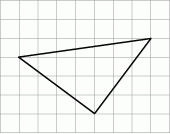
A) 76 B) 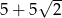 C)
C) 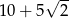 D) 75
D) 75
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
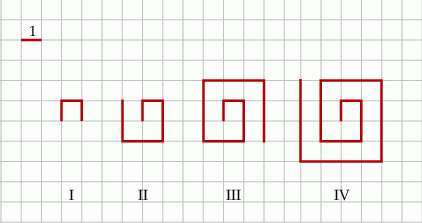
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 3 | 8 | 15 | 24 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 48 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 63 D) 80
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
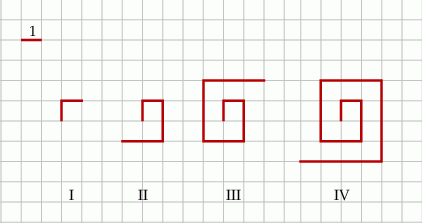
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 2 | 6 | 12 | 20 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 56 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 72 D) 80
Punkt 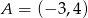 jest początkiem odcinka
jest początkiem odcinka 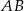 , gdzie
, gdzie 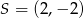 jest jego środkiem. Punkt
jest jego środkiem. Punkt 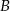 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 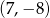 B)
B) 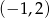 C)
C) 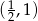 D)
D) 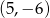
Punkt 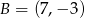 jest końcem odcinka
jest końcem odcinka 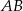 , gdzie
, gdzie 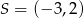 jest jego środkiem. Punkt
jest jego środkiem. Punkt 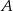 , który jest początkiem tego odcinka ma współrzędne
, który jest początkiem tego odcinka ma współrzędne
A) 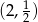 B)
B) 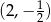 C)
C) 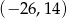 D)
D) 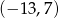
Punkt 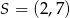 jest środkiem odcinka
jest środkiem odcinka 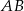 , w którym
, w którym 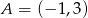 . Punkt
. Punkt 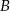 ma współrzędne:
ma współrzędne:
A) 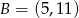 B)
B) 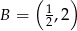 C)
C) 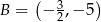 D)
D) 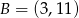
Punkt 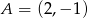 jest początkiem odcinka
jest początkiem odcinka 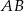 , gdzie
, gdzie 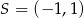 jest jego środkiem. Punkt
jest jego środkiem. Punkt 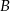 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 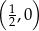 B)
B) 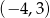 C)
C) 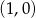 D)
D) 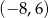
W układzie współrzędnych punkt 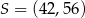 jest środkiem odcinka
jest środkiem odcinka 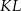 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 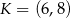 . Zatem
. Zatem
A) 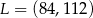 B)
B) 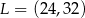 C)
C) 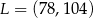 D)
D) 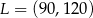
Punkt 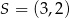 jest środkiem odcinka
jest środkiem odcinka 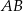 , w którym
, w którym 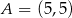 . Punkt
. Punkt 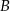 ma współrzędne
ma współrzędne
A) 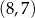 B)
B) 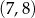 C)
C) 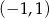 D)
D) 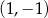
Punkt 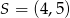 jest środkiem odcinka
jest środkiem odcinka 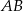 , w którym
, w którym 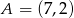 . Punkt
. Punkt 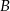 ma współrzędne:
ma współrzędne:
A) 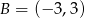 B)
B) 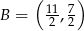 C)
C) 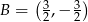 D)
D) 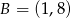
Punkt 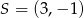 jest środkiem odcinka
jest środkiem odcinka 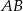 i
i 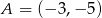 . Punkt
. Punkt 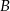 ma współrzędne
ma współrzędne
A) 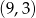 B)
B) 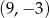 C)
C) 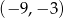 D)
D) 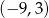
Punkt 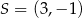 jest środkiem odcinka
jest środkiem odcinka 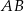 , w którym
, w którym 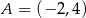 . Punkt
. Punkt 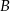 ma współrzędne
ma współrzędne
A) 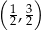 B)
B) 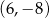 C)
C) 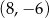 D)
D) 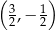
W układzie współrzędnych punkt 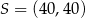 jest środkiem odcinka
jest środkiem odcinka 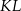 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 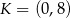 . Zatem
. Zatem
A) 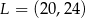 B)
B) 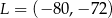 C)
C) 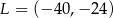 D)
D) 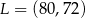
Punkt 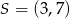 jest środkiem odcinka
jest środkiem odcinka 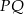 , gdzie
, gdzie 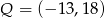 . Zatem punkt
. Zatem punkt 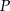 ma współrzędne
ma współrzędne
A) 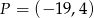 B)
B) 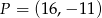 C)
C) 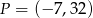 D)
D) 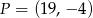
Punkt 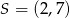 jest środkiem odcinka
jest środkiem odcinka 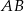 , w którym
, w którym 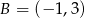 . Punkt
. Punkt 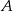 ma współrzędne:
ma współrzędne:
A) 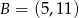 B)
B) 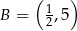 C)
C) 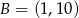 D)
D) 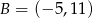
W układzie współrzędnych zaznaczono dwa punkty: 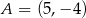 i
i 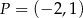 . Punkt
. Punkt 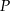 jest środkiem odcinka
jest środkiem odcinka 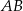 . Jakie współrzędne ma punkt B?
. Jakie współrzędne ma punkt B?
A) 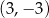 B)
B) 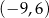 C)
C) 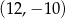 D)
D) 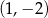
Dane są punkty 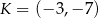 oraz
oraz 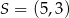 . Punkt
. Punkt 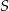 jest środkiem odcinka
jest środkiem odcinka 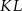 . Wtedy punkt
. Wtedy punkt 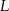 ma współrzędne
ma współrzędne
A) 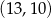 B)
B) 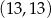 C)
C) 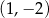 D)
D) 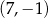
W układzie współrzędnych zaznaczono dwa punkty: 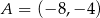 i
i 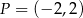 . Punkt
. Punkt 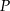 jest środkiem odcinka
jest środkiem odcinka 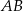 . Jakie współrzędne ma punkt
. Jakie współrzędne ma punkt 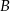 ?
?
A) 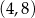 B)
B) 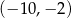 C)
C) 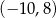 D)
D) 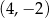
Punkt 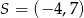 jest środkiem odcinka
jest środkiem odcinka 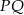 , gdzie
, gdzie 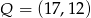 . Zatem punkt
. Zatem punkt 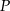 ma współrzędne
ma współrzędne
A) 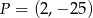 B)
B) 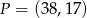 C)
C) 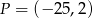 D)
D) 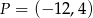
Punkt 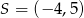 jest środkiem odcinka
jest środkiem odcinka 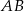 i
i 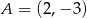 . Punkt
. Punkt 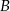 ma współrzędne
ma współrzędne
A) 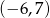 B)
B) 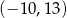 C)
C) 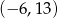 D)
D) 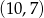
Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.
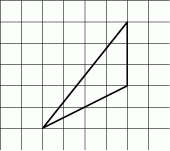
Pole narysowanego trójkąta jest równe
A) 3 B) 6 C) 12 D) 18
Na siatce kwadratowej narysowano równoległobok. Bok kwadratu siatki jest równy 1.
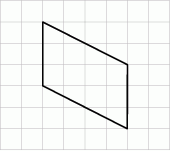
Pole narysowanego równoległoboku jest równe
A) 3 B) 6 C) 12 D) 18
Na siatce kwadratowej narysowano trapez. Bok kwadratu siatki jest równy 1.
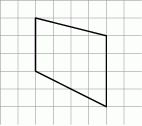
Pole narysowanego trapezu jest równe
A) 14 B) 7 C) 16 D) 12
W układzie współrzędnych zaznaczono wierzchołki 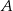 i
i 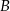 czworokąta
czworokąta 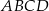 . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
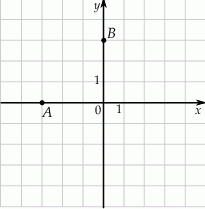
Pole czworokąta 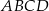 jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
W układzie współrzędnych zaznaczono wierzchołki 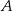 i
i 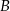 czworokąta
czworokąta  . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
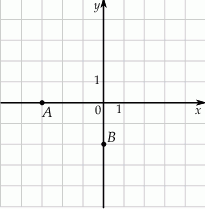
Pole czworokąta  jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
W układzie współrzędnych zaznaczono wierzchołki  i
i 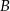 rombu
rombu 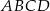 oraz jedną z jego osi symetrii.
oraz jedną z jego osi symetrii.
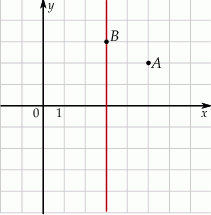
Pole rombu 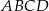 jest równe
jest równe
A) 2 B) 4 C) 6 D) 8
Na rysunku przedstawiono równoległobok  .
.
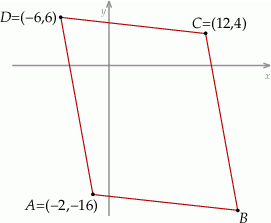
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek symetrii równoległoboku  ma współrzędne ma współrzędne 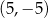 . . | P | F |
Wierzchołek 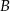 ma współrzędne ma współrzędne 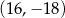 . . | P | F |
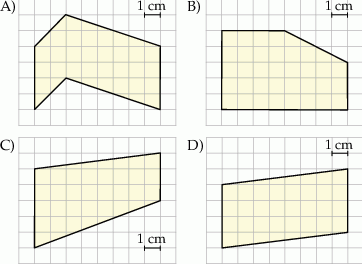
Na rysunkach zaznaczono cztery wielokąty o wierzchołkach w punktach przecięcia się linii siatki. Wskaż wielokąt, którego pole jest inne niż pola trzech pozostałych wielokątów.
W układzie współrzędnych zaznaczono wierzchołki sześciokąta 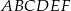 :
: 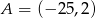 ,
, 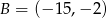 ,
, 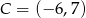 ,
, 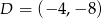 ,
, 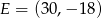 ,
, 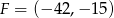 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trzy wierzchołki sześciokąta 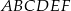 znajdują się w drugiej ćwiartce układu współrzędnych. znajdują się w drugiej ćwiartce układu współrzędnych. | P | F |
Dwa wierzchołki sześciokąta 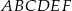 znajdują się w trzeciej ćwiartce układu współrzędnych. znajdują się w trzeciej ćwiartce układu współrzędnych. | P | F |
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 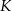 i
i 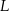 . Punkty te mają współrzędne
. Punkty te mają współrzędne 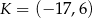 oraz
oraz 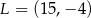 . Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka
. Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 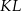 ?
?
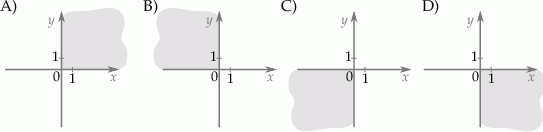
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 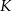 i
i 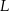 . Punkty te mają współrzędne
. Punkty te mają współrzędne 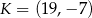 oraz
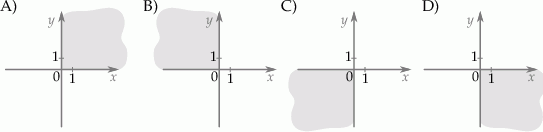
oraz 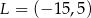 . Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka
. Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 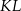 ?
?
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu  , które nie należą do tego samego boku.
, które nie należą do tego samego boku.
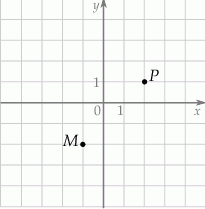
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
A) 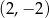 i
i 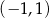 B)
B) 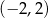 i
i 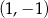 C)
C) 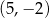 i
i 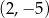 D)
D) 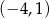 i
i 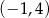
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu 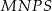 , które nie należą do tego samego boku.
, które nie należą do tego samego boku.
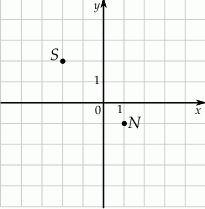
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
A) 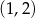 i
i 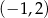 B)
B) 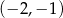 i
i 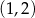 C)
C) 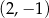 i
i 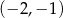 D)
D) 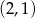 i
i 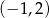
Punkty 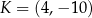 i
i 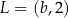 są końcami odcinka
są końcami odcinka 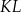 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 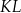 jest równa
jest równa 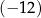 . Wynika stąd, że
. Wynika stąd, że
A) 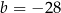 B)
B) 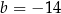 C)
C) 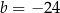 D)
D) 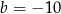
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 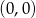 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  (rysunek).
(rysunek).
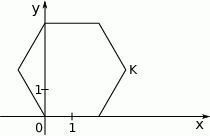
Współrzędne wierzchołka K tego sześciokąta są równe
A) 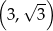 B)
B) 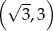 C)
C) 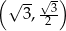 D)
D) 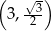
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 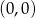 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 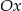 .
.
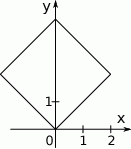
Długość boku kwadratu jest równa
A) 2 B) 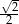 C)
C) 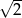 D)
D) 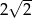
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 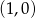 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 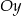 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 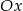 (zobacz rysunek).
(zobacz rysunek).
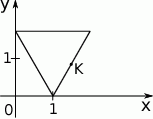
Współrzędne środka 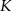 boku trójkąta są równe
boku trójkąta są równe
A) 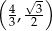 B)
B) 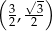 C)
C) 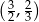 D)
D)