Punkt 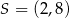 jest środkiem odcinka
jest środkiem odcinka 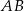 , gdzie
, gdzie 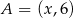 i
i 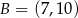 dla
dla  równego
równego
A) 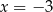 B)
B) 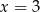 C)
C) 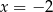 D)
D) 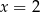
/Szkoła podstawowa/Zadania testowe/Geometria/Układ współrzędnych
W układzie współrzędnych zaznaczono punkt 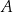 .
.

Punkt symetryczny do punktu 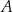 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 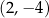 B)
B) 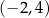 C)
C) 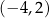 D)
D) 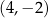
W układzie współrzędnych zaznaczono punkt 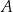 .
.

Punkt symetryczny do punktu 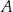 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 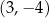 B)
B) 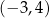 C)
C) 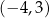 D)
D) 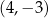
Punkty 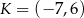 i
i 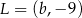 są końcami odcinka
są końcami odcinka 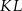 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 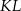 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 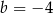 B)
B) 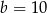 C)
C) 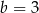 D)
D) 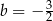
Zapoznaj się z rysunkiem przedstawiającym różne odcinki.
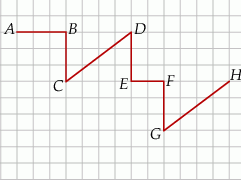
Uzupełnij zdania, korzystając z rysunku i podanych wyrazów. Zaznacz literę A lub B.
| A | prostopadłe |
| B | równoległe |
Odcinki 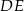 i i 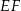 są są | A | B |
Odcinki 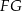 i i 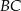 są są | A | B |
Odcinki 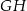 i i 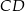 są są | A | B |
W układzie współrzędnych narysowano trapez równoramienny.
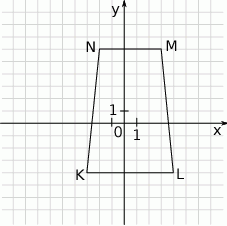
Równanie osi symetrii tego trapezu to
A) 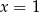 B)
B) 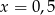 C)
C) 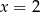 D)
D) 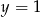
W układzie współrzędnych zaznaczono cztery kolejne wierzchołki sześciokąta 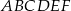 , który posiada środek symetrii.
, który posiada środek symetrii.
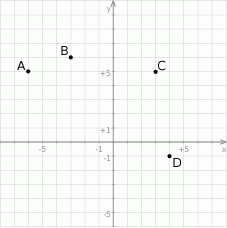
Który z podanych punktów jest jednym z wierzchołków tego sześciokąta?
A) 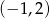 B)
B) 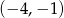 C)
C) 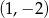 D)
D) 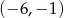
Punkty 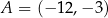 ,
, 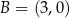 i
i 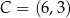 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 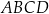 . Wierzchołek
. Wierzchołek 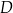 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 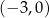 B)
B) 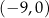 C)
C) 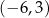 D)
D) 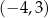
Na siatce kwadratowej narysowano czworokąt. Bok kwadratu siatki jest równy 1.
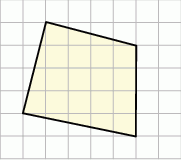
Pole narysowanego czworokąta jest równe
A) 18,5 B) 20 C) 21 D) 22
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
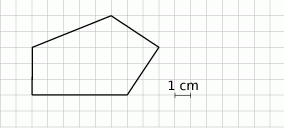
Pole tego wielokąta jest równe
A) 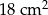 B)
B) 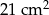 C)
C) 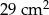 D)
D) 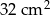
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
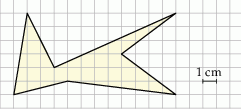
Pole tego wielokąta jest równe
A) 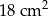 B)
B) 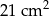 C)
C) 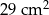 D)
D) 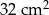
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
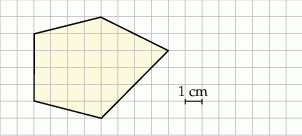
Pole tego wielokąta jest równe
A) 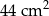 B)
B) 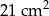 C)
C) 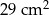 D)
D) 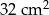
W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.
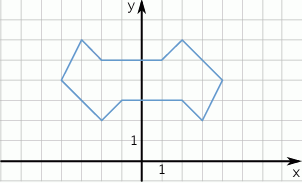
Przedstawiona figura
A) posiada jedną oś symetrii B) posiada dwie osie symetrii
C) posiada jeden środek symetrii D) posiada dwa środki symetrii
W prostokątnym układzie współrzędnych umieszczono figurę przedstawioną na rysunku.
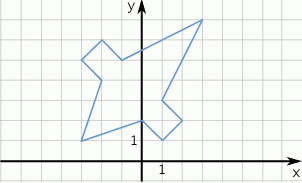
Przedstawiona figura
A) posiada jedną oś symetrii B) posiada dwie osie symetrii
C) posiada środek symetrii D) nie posiada osi symetrii
Wierzchołek 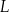 prostokąta przedstawionego na rysunku ma współrzędne
prostokąta przedstawionego na rysunku ma współrzędne

A) 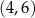 B)
B) 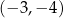 C)
C) 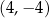 D)
D) 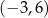
W układzie współrzędnych 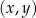 narysowano trapez
narysowano trapez 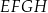 . Wszystkie współrzędne wierzchołków
. Wszystkie współrzędne wierzchołków 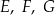 i
i 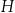 są liczbami całkowitymi.
są liczbami całkowitymi.
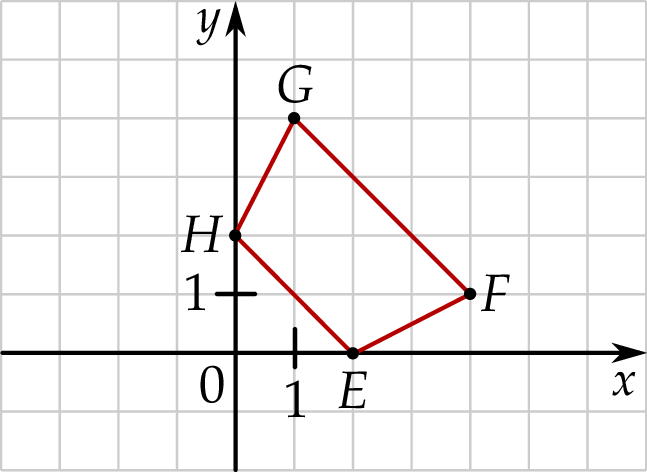
Punkty o współrzędnych 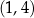 i
i 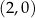 to wierzchołki
to wierzchołki
A) 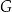 i
i 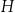 B)
B) 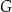 i
i 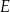 C)
C) 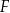 i
i 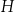 D)
D) 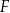 i
i 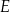
W układzie współrzędnych zaznaczono dwa wierzchołki prostokąta 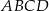 , które nie należą do tego samego boku. Boki tego prostokąta są równoległe do osi układu współrzędnych.
, które nie należą do tego samego boku. Boki tego prostokąta są równoległe do osi układu współrzędnych.
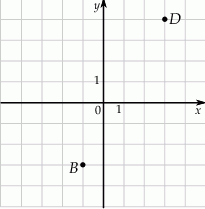
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta 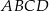 jest równe 28. jest równe 28. | P | F |
Obwód prostokąta 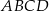 jest równy 11. jest równy 11. | P | F |
Punkty 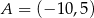 ,
, 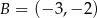 i
i 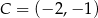 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 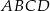 . Wierzchołek
. Wierzchołek 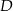 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 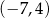 B)
B) 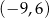 C)
C) 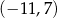 D)
D) 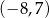
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 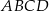 :
: 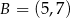 ,
, 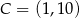 ,
, 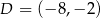 . Jakie współrzędne ma punkt A?
. Jakie współrzędne ma punkt A?
A) 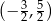 B)
B) 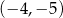 C)
C) 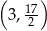 D)
D) 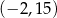
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki równoległoboku.
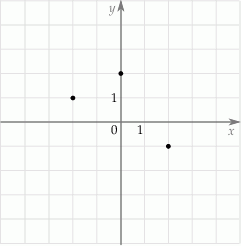
Który z punktów nie może być czwartym wierzchołkiem tego równoległoboku?
A) 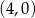 B)
B) 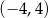 C)
C) 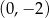 D)
D) 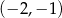
W układzie współrzędnych zaznaczono trójkąt 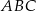 oraz punkt
oraz punkt 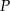 należący do boku
należący do boku 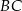 . Wszystkie współrzędne punktów
. Wszystkie współrzędne punktów 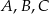 i
i 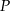 są liczbami całkowitymi.
są liczbami całkowitymi.
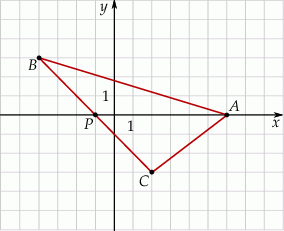
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 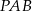 jest równe polu trójkąta jest równe polu trójkąta 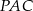 . . | P | F |
Pole trójkąta 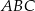 jest równe 21. jest równe 21. | P | F |
Wierzchołek 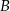 równoległoboku
równoległoboku 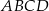 ma współrzędne
ma współrzędne
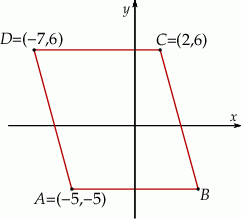
A) 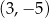 B)
B) 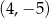 C)
C) 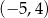 D)
D) 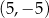
Na rysunku przedstawiono równoległobok 
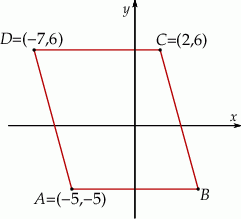
Pole równoległoboku 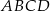 jest równe A/B.
jest równe A/B.
A) 99 B) 80
Wierzchołek 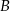 równoległoboku
równoległoboku 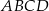 ma współrzędne C/D.
ma współrzędne C/D.
C) 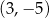 D)
D) 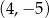
W układzie współrzędnych 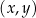 zaznaczono pięć punktów
zaznaczono pięć punktów 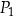 ,
, 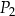 ,
, 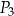 ,
, 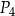 oraz
oraz 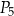 (zobacz rysunek). Wszystkie współrzędne tych punktów są liczbami całkowitymi. Punkt
(zobacz rysunek). Wszystkie współrzędne tych punktów są liczbami całkowitymi. Punkt 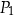 ma współrzędne
ma współrzędne 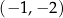 .
.

Jeżeli współrzędną  punktu
punktu 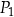 zwiększymy o 4, a współrzędną
zwiększymy o 4, a współrzędną 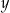 tego punktu zwiększymy o 3, to otrzymamy współrzędne punktu
tego punktu zwiększymy o 3, to otrzymamy współrzędne punktu
A) 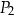 B)
B) 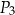 C)
C) 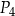 D)
D) 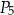
W układzie współrzędnych dane są punkty 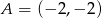 ,
, 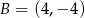 ,
, 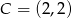 i
i 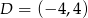 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Czworokąt 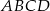 jest trapezem. jest trapezem. | P | F |
Czworokąt 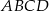 posiada oś symetrii. posiada oś symetrii. | P | F |
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta 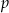 tak, jak na rysunku.
tak, jak na rysunku.
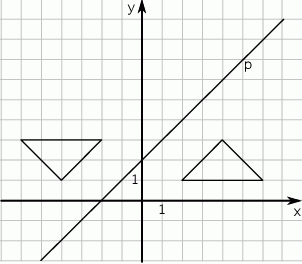
Jeden trójkąt jest symetryczny do drugiego względem
A) osi 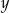
B) prostej 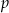
C) punktu 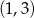
D) punktu przecięcia prostej 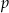 i osi
i osi 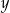 .
.
E) początku układu współrzędnych.
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta 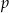 tak, jak na rysunku.
tak, jak na rysunku.
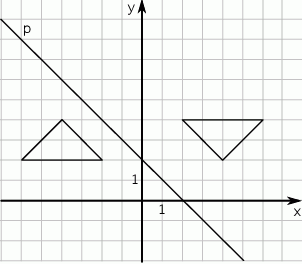
Jeden trójkąt jest symetryczny do drugiego względem
A) osi 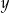 B) prostej
B) prostej 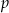
C) punktu 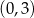 D) punktu przecięcia prostej
D) punktu przecięcia prostej 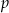 i osi
i osi 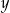 .
.
Jeżeli odcinek 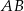 przecina oś
przecina oś 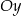 układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
A) 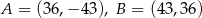 B)
B) 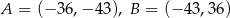
C) 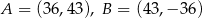 D)
D) 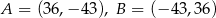
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 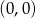 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
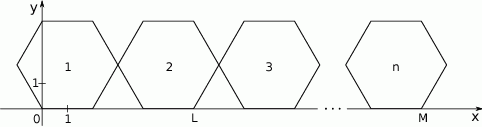
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 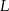 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 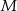 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 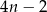 . . | P | F |
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 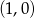 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 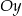 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 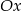 . Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi
. Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi 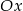 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
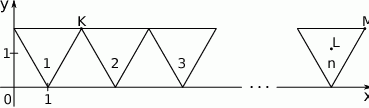
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek 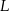 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 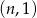 . . | P | F |
Wierzchołek 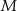 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 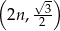 . . | P | F |
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 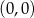 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 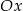 . Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi
. Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi 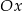 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
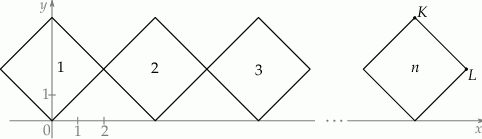
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 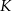 w w  –tym kwadracie jest równa –tym kwadracie jest równa 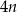 . . | P | F |
Pierwsza współrzędna wierzchołka 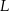 w w  –tym kwadracie jest równa –tym kwadracie jest równa 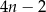 . . | P | F |

