Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 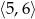 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 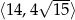 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Udowodnij
Punkt 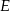 jest środkiem boku
jest środkiem boku 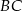 prostokąta
prostokąta 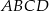 , w którym
, w którym 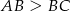 . Punkt
. Punkt 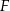 leży na boku
leży na boku 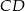 tego prostokąta oraz
tego prostokąta oraz 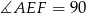 . Udowodnij, że
. Udowodnij, że 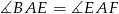 .
.
Dany jest prostokąt 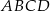 , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku
, którego jeden bok jest dwa razy dłuższy od drugiego. Na boku 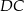 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 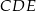 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 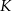 jest takim punktem odcinka
jest takim punktem odcinka 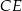 , że
, że 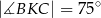 . Udowodnij, że punkt
. Udowodnij, że punkt 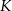 jest środkiem odcinka
jest środkiem odcinka 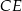 .
.
Punkt 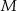 leży wewnątrz prostokąta
leży wewnątrz prostokąta 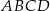 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 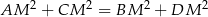 .
.
Dany jest prostokąt 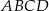 , którego boki mają długości
, którego boki mają długości  i
i 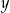 . Punkt
. Punkt 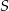 jest punktem przecięcia się przekątnych prostokąta.
jest punktem przecięcia się przekątnych prostokąta.
- Wykaż, że pole trójkąta
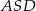 jest cztery razy mniejsze od pola prostokąta
jest cztery razy mniejsze od pola prostokąta 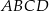 .
. - Wiedząc dodatkowo, że
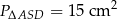 i
i 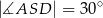 , oblicz pole kwadratu, którego bok ma długość
, oblicz pole kwadratu, którego bok ma długość 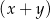 .
.
W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy
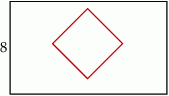
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.
- Wyraź pole pozostałe po wycięciu kwadratu z prostokąta jako funkcję dłuższego boku prostokąta. Wyznacz dziedzinę otrzymanej funkcji.
- Wykaż, że różnica pól prostokąta i kwadratu jest zawsze większa od 64.
Punkt 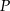 leży wewnątrz prostokąta
leży wewnątrz prostokąta  . Wykaż, że suma pól trójkątów
. Wykaż, że suma pól trójkątów  i
i 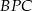 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 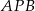 i
i 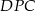 .
.
W prostokąt 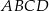 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 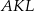 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 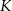 leży na boku
leży na boku 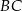 (
(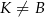 i
i 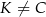 ), wierzchołek
), wierzchołek 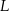 leży na boku
leży na boku 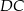 (
(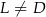 i
i 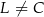 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 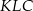 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 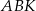 i
i 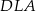 .
.
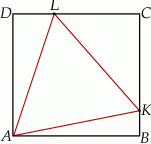
Dany jest prostokąt  . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt  jest styczny do przekątnej
jest styczny do przekątnej  w punkcie
w punkcie 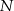 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 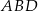 jest styczny do boku
jest styczny do boku 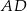 w punkcie
w punkcie 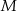 , a środek
, a środek 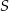 tego okręgu leży na odcinku
tego okręgu leży na odcinku 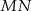 , jak na rysunku.
, jak na rysunku.
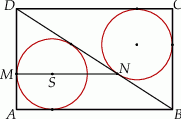
Wykaż, że 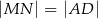 .
.
Dany jest prostokąt 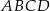 . Na boku
. Na boku 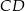 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 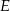 , że
, że 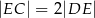 , a na boku
, a na boku 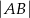 wybrano taki punkt
wybrano taki punkt 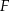 , że
, że 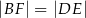 . Niech
. Niech 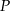 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 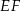 z prostą
z prostą 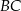 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 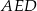 i
i 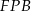 są przystające.
są przystające.
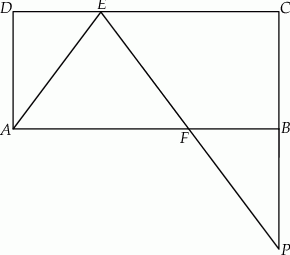
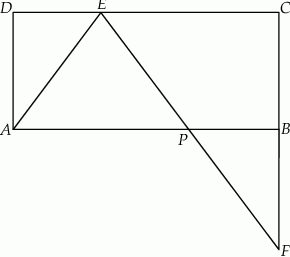
Dany jest prostokąt  . Na boku
. Na boku  tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt  , że
, że 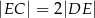 , a na przedłużeniu boku
, a na przedłużeniu boku  wybrano taki punkt
wybrano taki punkt  , że
, że 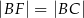 . Niech
. Niech 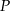 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 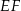 z prostą
z prostą 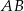 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 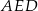 i
i 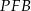 są przystające.
są przystające.
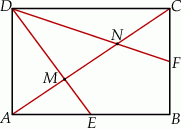
W prostokącie 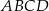 wierzchołek
wierzchołek  połączono odcinkami ze środkami
połączono odcinkami ze środkami 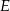 i
i 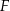 boków
boków 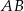 i
i 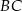 , zaś
, zaś 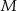 i
i 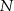 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 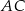 .
.
- Uzasadnij, że odcinki
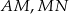 i
i 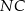 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
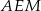 i
i 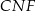 mają równe pola.
mają równe pola.
Na bokach 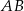 i
i 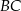 prostokąta
prostokąta 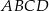 wybrano punkty
wybrano punkty 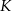 i
i 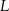 w ten sposób, że trójkąt
w ten sposób, że trójkąt 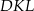 jest ostrokątny oraz
jest ostrokątny oraz 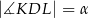 . Odcinek
. Odcinek 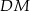 jest wysokością trójkąta
jest wysokością trójkąta 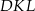 .
.
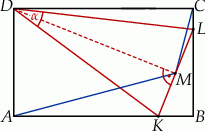
Wykaż, że 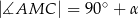 .
.
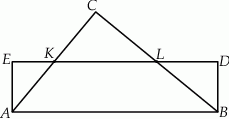
Na rysunku przedstawiono prostokąt 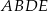 i trójkąt
i trójkąt 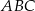 . Punkty
. Punkty 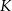 i
i 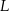 dzielą odcinki
dzielą odcinki 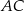 i
i 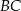 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 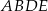 jest równe polu trójkąta
jest równe polu trójkąta 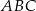 .
.
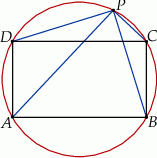
Punkt 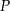 należy do okręgu opisanego na prostokącie
należy do okręgu opisanego na prostokącie 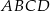 . Wykaż, że
. Wykaż, że 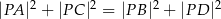 .
.
Punkt 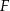 jest środkiem boku
jest środkiem boku 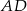 prostokąta
prostokąta 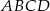 , w którym
, w którym 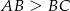 . Punkt
. Punkt 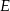 jest takim punktem boku
jest takim punktem boku 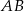 tego prostokąta, że prosta
tego prostokąta, że prosta 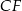 jest dwusieczną kąta
jest dwusieczną kąta 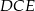 . Wykaż, że trójkąt
. Wykaż, że trójkąt 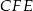 jest prostokątny.
jest prostokątny.
W prostokącie 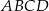 punkt
punkt 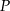 jest środkiem boku
jest środkiem boku 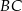 , a punkt
, a punkt 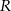 jest środkiem boku
jest środkiem boku 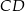 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 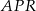 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 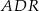 oraz
oraz 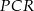 .
.
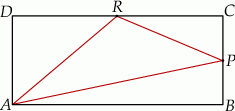
W prostokącie 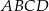 punkt
punkt 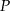 jest środkiem boku
jest środkiem boku 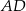 , a punkt
, a punkt 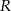 jest środkiem boku
jest środkiem boku 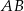 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 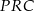 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 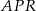 oraz
oraz 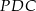 .
.
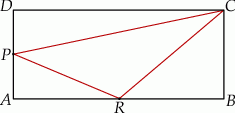
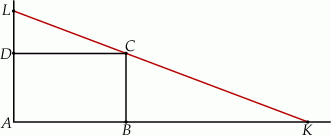
Przez wierzchołek  prostokąta
prostokąta 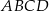 poprowadzono prostą, która przecięła proste
poprowadzono prostą, która przecięła proste 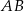 i
i 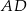 w punktach
w punktach 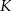 i
i 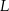 odpowiednio. Wykaż, że
odpowiednio. Wykaż, że 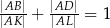 .
.
Uzasadnij, że jeżeli prostokąt 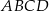 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.


