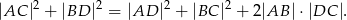Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Wykaż, że w dowolnym trapezie suma długości ramion jest mniejsza od sumy długości przekątnych.
Przekątne czworokąta 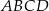 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 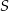 , a punkt
, a punkt 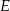 jest takim punktem przekątnej
jest takim punktem przekątnej 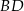 , że
, że 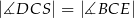 (zobacz rysunek).
(zobacz rysunek).
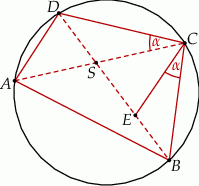
Wykaż, że 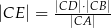 .
.
Wysokość trapezu równoramiennego ma długość 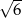 , a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
, a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
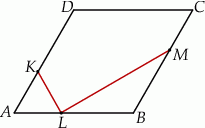
Bok rombu 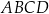 ma długość
ma długość  , a sinus jego kąta ostrego
, a sinus jego kąta ostrego 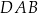 jest równy
jest równy 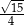 . Na bokach
. Na bokach 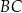 i
i 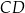 wybrano punkty
wybrano punkty 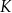 i
i 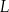 odpowiednio tak, że odcinki
odpowiednio tak, że odcinki 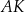 i
i 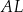 podzieliły pole rombu
podzieliły pole rombu 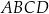 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
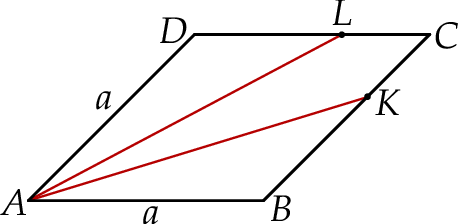
Oblicz długość odcinka 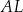 .
.
Wykaż, że jeśli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego, to ramię jest równe krótszej podstawie.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego wynosi 50 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 5 cm i 12 cm. Oblicz pole trapezu.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że pola tych trójkątów, w których jeden z boków jest ramieniem trapezu, są równe.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól tych trójkątów, w których jeden z boków jest podstawą trapezu, jest równy stosunkowi kwadratów długości podstaw trapezu.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól trójkątów takich, że bokiem jednego jest ramię trapezu, a bokiem drugiego jest podstawa trapezu, jest równy stosunkowi długości podstaw trapezu.
W czworokącie 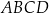 dane są długości boków:
dane są długości boków: 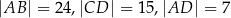 . Ponadto kąty
. Ponadto kąty 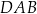 oraz
oraz 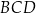 są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Dany jest prostokąt 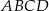 , którego boki mają długości
, którego boki mają długości  i
i 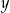 . Punkt
. Punkt 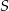 jest punktem przecięcia się przekątnych prostokąta.
jest punktem przecięcia się przekątnych prostokąta.
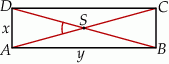
- Wykaż, że pole trójkąta
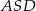 jest cztery razy mniejsze od pola prostokąta
jest cztery razy mniejsze od pola prostokąta 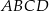 .
. - Wiedząc dodatkowo, że
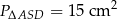 i
i 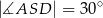 , oblicz pole kwadratu, którego bok ma długość
, oblicz pole kwadratu, którego bok ma długość 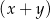 .
.
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
Na bokach 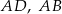 i
i 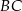 rombu
rombu 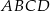 wybrano punkty
wybrano punkty 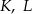 i
i 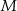 w ten sposób, że
w ten sposób, że 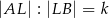 oraz
oraz 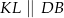 ,
, 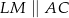 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 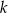 , dla których pole pięciokąta
, dla których pole pięciokąta 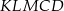 stanowi
stanowi 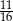 pola rombu.
pola rombu.
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 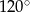 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
Krótsza przekątna rombu o długości 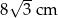 dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
Czworokąt 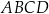 jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach
jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach 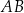 i
i 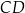 są styczne zewnętrznie, to równoległobok
są styczne zewnętrznie, to równoległobok 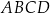 jest rombem.
jest rombem.
Prosta przechodząca przez wierzchołek 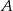 równoległoboku
równoległoboku 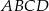 przecina jego przekątną
przecina jego przekątną 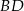 w punkcie
w punkcie 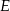 i bok
i bok 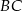 w punkcie
w punkcie 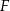 , a prostą
, a prostą 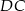 w punkcie
w punkcie 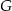 . Udowodnij, że
. Udowodnij, że
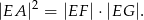
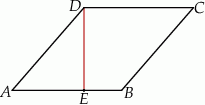
Wysokość 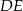 rombu
rombu 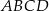 dzieli bok
dzieli bok 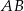 tego rombu tak, że
tego rombu tak, że 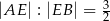 (zobacz rysunek).
(zobacz rysunek).
Oblicz wartość wyrażenia
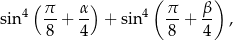
gdzie  i
i 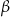 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu 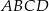 .
.
Prosta przechodząca przez wierzchołek 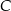 kwadratu
kwadratu 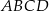 przecina przedłużenia jego boków
przecina przedłużenia jego boków 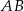 i
i 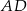 odpowiednio w punktach
odpowiednio w punktach 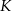 i
i 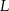 (zobacz rysunek).
(zobacz rysunek).
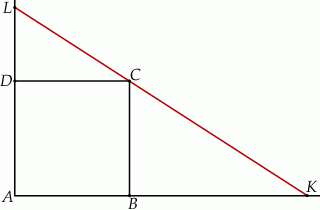
Wykaż, że
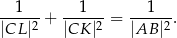
W czworokącie 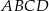 spełniony jest warunek
spełniony jest warunek 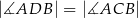 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 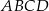 można opisać okrąg.
można opisać okrąg.
Dany jest prostokąt 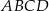 , w którym
, w którym 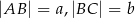 i
i 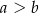 . Odcinek
. Odcinek 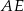 jest wysokością trójkąta
jest wysokością trójkąta 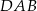 opuszczoną na jego bok
opuszczoną na jego bok 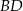 . Wyraź pole trójkąta
. Wyraź pole trójkąta 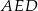 za pomocą
za pomocą  i
i 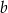 .
.
Dany jest kwadrat 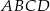 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka 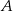 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
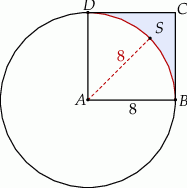
Oblicz pole powierzchni obszaru 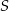 otrzymanego z kwadratu
otrzymanego z kwadratu 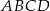 przez wycięcie części pokrytej kołem.
przez wycięcie części pokrytej kołem.
Czworokąt 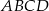 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 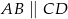 . Wykaż że
. Wykaż że