Na rysunku przedstawiono kwadrat 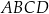 o polu 4.
o polu 4.

Punkty 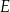 i
i 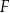 są środkami boków
są środkami boków 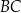 i
i 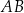 , a punkt
, a punkt 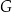 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 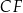 i
i 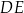 . Oblicz pole czworokąta
. Oblicz pole czworokąta 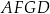
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono kwadrat 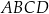 o polu 4.
o polu 4.

Punkty 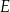 i
i 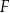 są środkami boków
są środkami boków 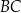 i
i 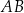 , a punkt
, a punkt 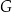 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 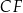 i
i 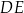 . Oblicz pole czworokąta
. Oblicz pole czworokąta 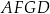
Dany jest czworokąt o kolejnych bokach długości 3,4,5 oraz kącie  między bokami długości 3 i 4 takim, że
między bokami długości 3 i 4 takim, że 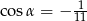 . Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
. Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
Obwód trapezu równoramiennego opisanego na okręgu jest równy 16, a przekątna trapezu ma długość 5. Oblicz długość promienia okręgu wpisanego w ten trapez i promienia okręgu opisanego na nim.
Dwa przeciwległe boki kwadratu wydłużono dwukrotnie, a każdy z dwóch pozostałych skrócono o 3 cm. Pole otrzymanego prostokąta jest o 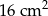 większe od pola kwadratu. Oblicz długości boków prostokąta.
większe od pola kwadratu. Oblicz długości boków prostokąta.
Dwa przeciwległe boki kwadratu wydłużono trzykrotnie, a każdy z dwóch pozostałych wydłużono o 2 cm. Pole otrzymanego prostokąta jest o 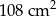 większe od pola kwadratu. Oblicz długości boków prostokąta.
większe od pola kwadratu. Oblicz długości boków prostokąta.
Na bokach 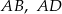 i
i 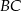 rombu
rombu 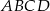 wybrano odpowiednio punkty
wybrano odpowiednio punkty 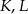 i
i 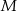 w ten sposób, że odcinki
w ten sposób, że odcinki 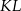 i
i 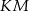 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 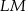 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Przekątne trapezu równoramiennego 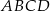 przecinają się w punkcie
przecinają się w punkcie 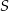 . Przekątna
. Przekątna 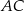 tworzy z dłuższą podstawą
tworzy z dłuższą podstawą 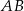 kąt
kąt  i z ramieniem
i z ramieniem 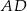 kąt
kąt 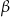 takie, że
takie, że 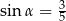 i
i 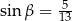 . Pole trapezu
. Pole trapezu 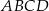 jest równe 448. Oblicz pole trójkąta
jest równe 448. Oblicz pole trójkąta 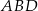 .
.
Stosunek długości ramion trapezu opisanego na okręgu o promieniu 6 cm wynosi 3:4. Obwód trapezu jest równy 70 cm. Oblicz długości podstaw trapezu.
Długości podstaw trapezu równoramiennego są równe  oraz
oraz 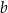 , przy czym
, przy czym 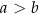 . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od
. W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od 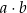 .
.
Czworokąt 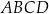 , w którym
, w którym 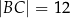 i
i 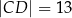 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 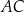 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 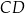 kąt, którego tangens jest równy
kąt, którego tangens jest równy 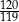 . Tangens kąta
. Tangens kąta 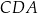 jest równy
jest równy 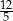 . Oblicz długość odcinka
. Oblicz długość odcinka 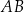 .
.
Oblicz pole rombu, w którym długość boku jest równa 13 cm, a długości przekątnych różnią się o 14 cm.
Oblicz pole rombu o obwodzie 68 cm, w którym długości przekątnych różnią się o 14 cm.
Obwód rombu jest równy 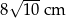 , a jedna z jego przekątnych jest o 8 cm dłuższa od drugiej. Oblicz pole rombu.
, a jedna z jego przekątnych jest o 8 cm dłuższa od drugiej. Oblicz pole rombu.
Dany jest romb o boku długości 35. Długości przekątnych tego rombu różnią się o 14. Oblicz pole tego rombu.
W trapez 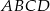 , gdzie
, gdzie 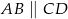 i
i 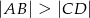 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
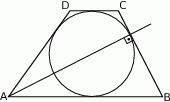
Dwusieczna kąta ostrego przy wierzchołku 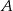 jest prostopadła do ramienia
jest prostopadła do ramienia 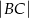 .
.
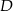 jest równoległa do ramienia
jest równoległa do ramienia 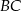 .
. 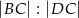 .
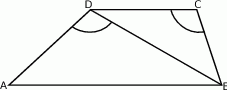
.W trapezie 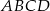 długość podstawy
długość podstawy 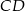 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 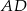 i
i 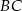 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty 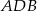 i
i 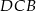 , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
Na kole opisany jest romb. Stosunek pola koła do pola powierzchni rombu wynosi 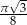 . Wyznacz miarę kąta ostrego rombu.
. Wyznacz miarę kąta ostrego rombu.
Podstawy trapezu mają długości 10 i 6. Wiedząc, że suma miar kątów wewnętrznych przy dłuższej podstawie jest równa 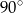 , oblicz długość odcinka łączącego środki podstaw trapezu.
, oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu 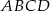 mają długości
mają długości 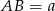 i
i 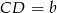 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 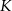 i
i 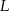 w ten sposób, że odcinek
w ten sposób, że odcinek 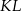 jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka
jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 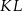 .
.
W romb o boku długości 10 cm i wysokości 8 cm wpisano okrąg 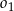 .
.
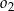 i wyznacz długość promienia tego okręgu.
i wyznacz długość promienia tego okręgu. 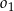 i
i 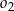 w skali 1:2.
w skali 1:2.Długości boków równoległoboku są równe 6 i 10, a jego pole wynosi 36. Oblicz długości przekątnych tego równoległoboku.
Długości boków równoległoboku są równe 13 i 21, a jego pole wynosi 252. Oblicz długości przekątnych tego równoległoboku.
W czworokącie wypukłym 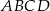 dane są długości jego boków i miara kąta
dane są długości jego boków i miara kąta 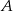 . Wyznacz miary pozostałych kątów tego czworokąta.
. Wyznacz miary pozostałych kątów tego czworokąta.
Dany jest równoległobok, którego obwód jest równy 50 cm. Stosunek długości jego wysokości wynosi 2:3, a stosunek miar jego kątów wewnętrznych jest równy 1:2. Oblicz długości boków i wysokości tego równoległoboku.
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
