Ze zbioru pięciu liczb 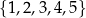 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 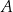 polegającego na tym, że obie wylosowane liczby są nieparzyste.
polegającego na tym, że obie wylosowane liczby są nieparzyste.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 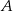 polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
Wzór funkcji 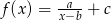 tworzymy w następujący sposób. Ze zbioru
tworzymy w następujący sposób. Ze zbioru
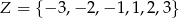
losujemy kolejno 3 liczby (bez zwracania); pierwsza z wylosowanych liczb jest równa współczynnikowi  , druga – współczynnikowi
, druga – współczynnikowi 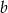 , trzecia – współczynnikowi
, trzecia – współczynnikowi  . Oblicz prawdopodobieństwo zdarzeń:
. Oblicz prawdopodobieństwo zdarzeń:
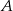 – funkcja
– funkcja 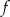 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 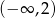 oraz
oraz 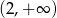 ;
; 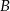 – miejscem zerowym funkcji
– miejscem zerowym funkcji 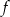 jest 0.
jest 0. 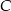 – funkcja
– funkcja 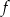 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 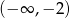 oraz
oraz 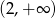 ;
;
Ze zbioru liczb 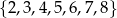 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 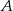 polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
Ze zbioru liczb 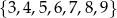 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 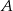 polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
Ze zbioru sześciu liczb 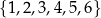 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 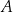 polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 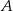 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 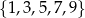 , i jednocześnie cyfrę jedności, która należy do zbioru
, i jednocześnie cyfrę jedności, która należy do zbioru 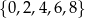 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 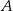 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
Ze zbioru 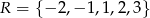 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 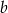 . Liczby
. Liczby  i
i 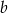 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 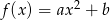 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
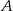 – funkcja
– funkcja 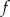 jest malejąca w zbiorze
jest malejąca w zbiorze 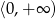 ,
, 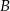 – funkcja
– funkcja 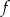 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru 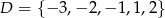 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 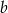 . Liczby
. Liczby  i
i 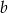 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 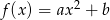 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
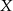 – funkcja
– funkcja 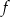 jest malejąca w zbiorze
jest malejąca w zbiorze 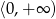 ,
, 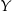 – funkcja
– funkcja 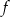 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru liczb: 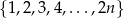 , gdzie
, gdzie 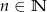 i
i 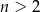 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 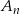 oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a
oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a 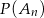 prawdopodobieństwo zajścia zdarzenia
prawdopodobieństwo zajścia zdarzenia 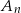 . Oblicz:
. Oblicz: 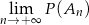 .
.
Ze zbioru 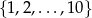 losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki
losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki 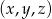 liczb, dla której
liczb, dla której 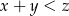 .
.
Ze zbioru cyfr 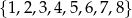 losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 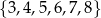 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 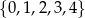 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
W dwóch pojemnikach znajdują się ponumerowane kule. W pierwszym pojemniku są kule z numerami: 1, 2, 3, 4, 5, w drugim z numerami: 4, 5, 6, 7, 8, 9. Losujemy po jednej kuli z każdego pojemnika i tworzymy liczbę dwucyfrową. Numer kuli wylosowanej z pierwszego pojemnika jest cyfrą dziesiątek, numer kuli wylosowanej z drugiego pojemnika jest cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że utworzona liczba jest podzielna przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 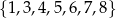 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 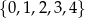 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 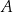 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 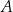 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 7 kul ponumerowanych kolejnymi liczbami od 2 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 9.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 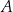 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia 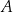 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Ze zbioru 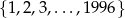 losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
- 6
- 4 lub 6
- 4 lub 6 lub 10
Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru siedmiu liczb naturalnych 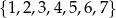 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
Ze zbioru ośmiu liczb naturalnych 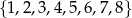 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
Ze zbioru liczb 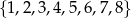 wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
Niech 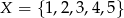 i
i 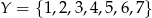 . Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji
. Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji 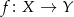 jest dwuelementowy.
jest dwuelementowy.
Losujemy dwie różne liczby całkowite  i
i 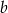 z przedziału
z przedziału 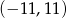 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 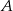 – równanie
– równanie 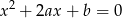 nie ma rozwiązań.
nie ma rozwiązań.
Z ustalonego zbioru  liczb rzeczywistych losujemy kolejno
liczb rzeczywistych losujemy kolejno 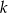 liczb, otrzymując ciąg różnowartościowy
liczb, otrzymując ciąg różnowartościowy 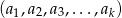 . Zakładając, że
. Zakładając, że 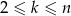 , oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
, oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
Z cyfr 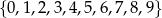 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
Z cyfr 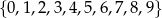 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.
Z cyfr 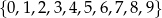 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
Ze zbioru liczb 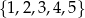 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 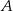 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 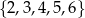 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 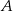 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 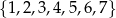 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 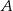 polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
Ze zbioru 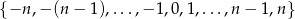 , gdzie
, gdzie 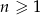 losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż
losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż  .
.

