Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 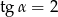 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 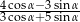 .
.
/Szkoła średnia/Funkcje/Trygonometryczna
Kąt  jest ostry i
jest ostry i 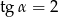 . Oblicz
. Oblicz 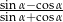 .
.
Oblicz wartość wyrażenia 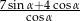 jeżeli
jeżeli  jest takim kątem ostrym, że
jest takim kątem ostrym, że 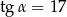 .
.
Oblicz wartość wyrażenia 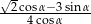 wiedząc, że
wiedząc, że 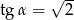 i
i 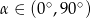 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 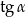 =3, oblicz wartość wyrażenia
=3, oblicz wartość wyrażenia 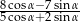 .
.
Wykaż, że dla dowolnego kąta  prawdziwa jest tożsamość
prawdziwa jest tożsamość 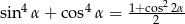 .
.
- Sprawdź, czy równość
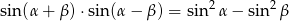
jest tożsamością trygonometryczną.
- Udowodnij, że jeżeli
 i
i 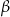 są dwoma kątami trójkąta i
są dwoma kątami trójkąta i 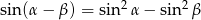 , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
, to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Oblicz wartość wyrażenia 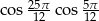 .
.
Wyznacz zbiór wartości funkcji 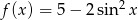 dla
dla 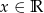 .
.
Wyznacz zbiór wartości funkcji 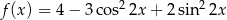 dla
dla 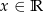 .
.
Wyznacz okres podstawowy funkcji 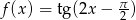 .
.
Wyznacz okres podstawowy funkcji 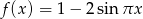 .
.
Wyznacz okres podstawowy funkcji 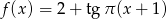 .
.
Wyznacz okres podstawowy funkcji 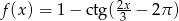 .
.
Wiedząc, że 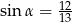 i
i 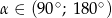 , oblicz
, oblicz 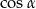 oraz
oraz 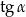 .
.
Oblicz 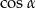 oraz
oraz 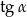 , jeżeli
, jeżeli 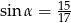 i
i 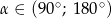 .
.
Wiedząc, że 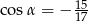 i
i 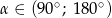 , oblicz
, oblicz 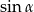 oraz
oraz 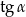 .
.
Wyznacz największą wartość funkcji
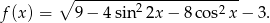
Uzasadnij, że jeżeli 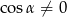 to prawdą jest, że
to prawdą jest, że 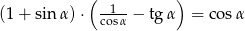 .
.
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
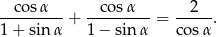
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
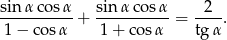
Wykaż, że dla każdego kąta ostrego  prawdziwy jest wzór
prawdziwy jest wzór 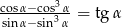 .
.
Wykaż, że 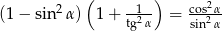 .
.
Uzasadnij, że dana równość 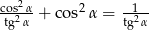 jest prawdziwa.
jest prawdziwa.
Wykaż, że 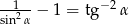 .
.
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
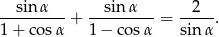
Wykaż tożsamość 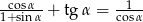 .
.
Kąt  jest ostry i
jest ostry i 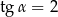 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 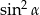 .
.
Wiedząc, że 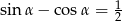 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 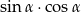 .
.
Wiedząc, że 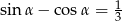 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 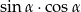 .
.
Wyznacz zbiór wartości funkcji 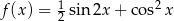 , gdzie
, gdzie 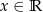 .
.
Wykaż, że nie istnieje kąt ostry  taki, że
taki, że 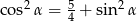 .
.
Wykaż, że dla dowolnego kąta  takiego, że
takiego, że 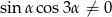 zachodzi tożsamość
zachodzi tożsamość
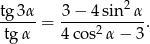
Wykaż, że 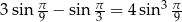 .
.
Dana jest funkcja 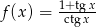 dla
dla 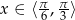 .
.
- Rozwiąż równanie
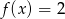 .
. - Wyznacz najmniejszą wartość funkcji
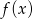 .
.
Wykaż, że wyrażenie 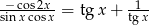 nie jest tożsamością.
nie jest tożsamością.
Udowodnij, że jeżeli 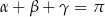 , to
, to
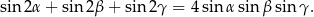
Wykaż, że wszystkie wartości funkcji 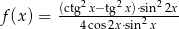 są większe od 1.
są większe od 1.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 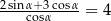 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 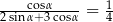 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 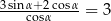 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.

