W okrąg o równaniu 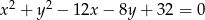 wpisano trójkąt równoboczny
wpisano trójkąt równoboczny  w którym
w którym 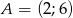 . Oblicz współrzędne pozostałych wierzchołków trójkąta.
. Oblicz współrzędne pozostałych wierzchołków trójkąta.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny
Dany jest wierzchołek trójkąta równobocznego 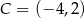 . Bok
. Bok 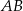 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 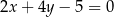 . Wyznacz długość boku tego trójkąta.
. Wyznacz długość boku tego trójkąta.
Punkt 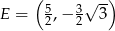 jest środkiem boku
jest środkiem boku 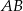 trójkąta równobocznego
trójkąta równobocznego 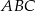 , a boki
, a boki 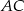 i
i 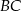 tego trójkąta są zawarte odpowiednio w prostych o równaniach
tego trójkąta są zawarte odpowiednio w prostych o równaniach 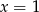 i
i 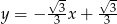 . Wyznacz współrzędne wierzchołków tego trójkąta.
. Wyznacz współrzędne wierzchołków tego trójkąta.
Podstawa 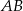 trójkąta równobocznego
trójkąta równobocznego 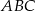 zawarta jest w prostej
zawarta jest w prostej 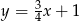 , a wierzchołek
, a wierzchołek 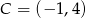 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 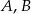 tego trójkąta.
tego trójkąta.
Wierzchołki trójkąta równobocznego 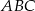 są punktami paraboli
są punktami paraboli 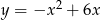 . Punkt
. Punkt 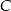 jest jej wierzchołkiem, a bok
jest jej wierzchołkiem, a bok 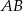 jest równoległy do osi
jest równoległy do osi 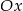 . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
. Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
W trójkąt równoboczny 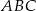 wpisano okrąg o środku w punkcie
wpisano okrąg o środku w punkcie 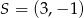 . Wiedząc, że wierzchołek
. Wiedząc, że wierzchołek 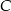 ma współrzędne
ma współrzędne 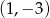 wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
Punkt 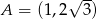 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 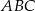 . Bok
. Bok 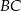 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 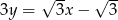 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 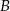 i
i 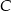 trójkąta.
trójkąta.
Dane są punkty 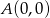 i
i 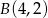 .
.
- Znajdź takie punkty
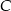 i
i 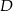 aby trójkąty
aby trójkąty 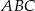 i
i 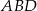 były równoboczne.
były równoboczne. - Znajdź równanie okręgu wpisanego w romb
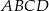 .
. - Oblicz pole figury, którą otrzymamy po usunięciu z rombu
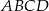 wnętrza wpisanego w niego koła.
wnętrza wpisanego w niego koła.
Dany jest trójkąt równoboczny 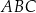 , w którym
, w którym 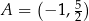 . Bok
. Bok 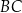 tego trójkąta jest zwarty w prostej o równaniu
tego trójkąta jest zwarty w prostej o równaniu 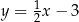 . Oblicz współrzędne środka odcinka
. Oblicz współrzędne środka odcinka 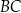 oraz oblicz pole trójkąta
oraz oblicz pole trójkąta 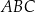 .
.
W trójkącie równobocznym 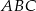 dane są wierzchołek
dane są wierzchołek 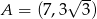 i środek okręgu wpisanego
i środek okręgu wpisanego 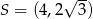 . Oblicz pole trójkąta
. Oblicz pole trójkąta 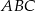 .
.
Punkt 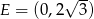 jest środkiem boku
jest środkiem boku 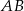 trójkąta równobocznego
trójkąta równobocznego 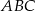 , prosta
, prosta 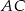 ma równanie
ma równanie 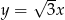 , a początek układu współrzędnych pokrywa się wierzchołkiem
, a początek układu współrzędnych pokrywa się wierzchołkiem 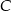 tego trójkąta. Napisz równania wysokości trójkąta
tego trójkąta. Napisz równania wysokości trójkąta 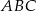 przechodzących przez wierzchołki
przechodzących przez wierzchołki 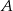 i
i 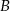 .
.
Napisz równanie okręgu stycznego do osi 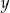 w punkcie
w punkcie 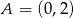 i przechodzącego przez punkt
i przechodzącego przez punkt 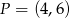 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 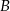 i
i 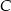 , aby trójkąt
, aby trójkąt 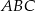 był równoboczny.
był równoboczny.
Odcinek 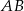 jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że
jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że 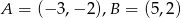
Punkty 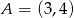 ,
, 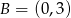 i
i 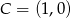 należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
Dany jest okrąg 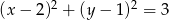 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
. Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.

