Oblicz pole i obwód trójkąta o wierzchołkach: 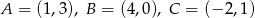 .
.
/Szkoła średnia/Geometria/Geometria analityczna
W okrąg o równaniu 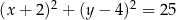 wpisano trójkąt
wpisano trójkąt 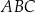 , którego pole jest równe 20. Bok
, którego pole jest równe 20. Bok 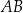 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 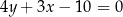 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 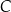 przecina bok
przecina bok 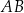 w punkcie
w punkcie 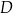 , którego obie współrzędne są dodatnie. Oblicz współrzędne punktu
, którego obie współrzędne są dodatnie. Oblicz współrzędne punktu 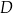 .
.
Przekątne 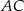 i
i 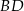 rombu
rombu 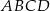 przecinają się w punkcie
przecinają się w punkcie 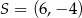 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 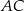 wiedząc, że prosta zawierająca przekątną
wiedząc, że prosta zawierająca przekątną 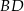 ma równanie
ma równanie 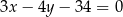 .
.
Przekątne rombu 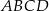 przecinają się w punkcie
przecinają się w punkcie 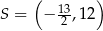 . Punkty
. Punkty 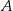 i
i 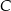 leżą na prostej o równaniu
leżą na prostej o równaniu 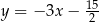 . Wyznacz równanie prostej
. Wyznacz równanie prostej 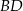 .
.
Przekątne rombu 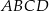 przecinają się w punkcie
przecinają się w punkcie 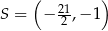 . Punkty
. Punkty 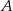 i
i 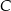 leżą na prostej o równaniu
leżą na prostej o równaniu 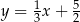 . Wyznacz równanie prostej
. Wyznacz równanie prostej 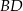 .
.
Napisz równanie okręgu stycznego do osi 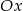 układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej
układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej 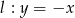 i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do
i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do 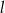 .
.
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/2293968/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 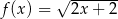 i
i 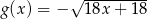 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 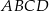 , których wierzchołki
, których wierzchołki 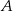 i
i 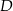 leżą na wykresie funkcji
leżą na wykresie funkcji 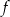 , a wierzchołki
, a wierzchołki 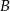 i
i 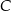 leżą na wykresie funkcji
leżą na wykresie funkcji 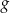 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 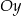 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że jeżeli pierwsza współrzędna punktów 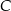 i
i 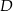 jest równa 7, a druga współrzędna punktu
jest równa 7, a druga współrzędna punktu 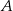 jest równa
jest równa 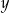 , to pole trapezu
, to pole trapezu 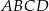 jest równe
jest równe
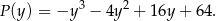
Dany jest okrąg 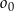 o równaniu
o równaniu 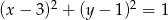 . W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi 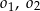 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 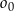 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 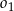 oraz
oraz 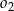 .
.
Dany jest okrąg 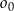 o równaniu
o równaniu 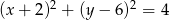 . W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi 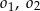 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 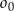 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 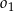 oraz
oraz 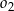 .
.
Punkt 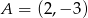 jest wierzchołkiem rombu
jest wierzchołkiem rombu 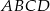 o polu równym 300. Punkt
o polu równym 300. Punkt 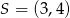 jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Czworokąt 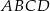 jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki
jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki 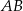 i
i 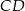 , przy czym
, przy czym 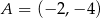 ,
, 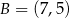 i
i 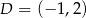 , oblicz pole oraz obwód trapezu.
, oblicz pole oraz obwód trapezu.
Dany jest okrąg o równaniu 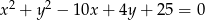 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
. Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
Wyznacz równania stycznych do okręgu 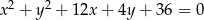 , przechodzących przez początek układu współrzędnych.
, przechodzących przez początek układu współrzędnych.
Okrąg o środku 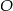 jest wpisany w trójkąt
jest wpisany w trójkąt 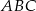 , gdzie
, gdzie 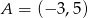 . Wiedząc, że okrąg ten jest styczny do boków
. Wiedząc, że okrąg ten jest styczny do boków 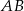 i
i 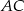 odpowiednio w punktach
odpowiednio w punktach 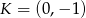 i
i 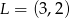 oblicz długość odcinka
oblicz długość odcinka 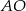 .
.
Punkty przecięcia paraboli 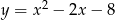 z prostą
z prostą 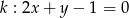 są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
Punkty 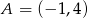 oraz
oraz 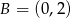 należą do prostej
należą do prostej 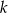 . Punkt
. Punkt 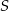 ma współrzędne
ma współrzędne 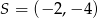 . Oblicz współrzędne punktów należących do prostej
. Oblicz współrzędne punktów należących do prostej 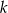 , których odległość od punktu
, których odległość od punktu 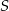 wynosi 5.
wynosi 5.
Znajdź równanie prostej, zawierającą dwusieczną tego kąta, utworzonego przez proste 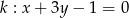 oraz
oraz 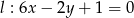 , do obszaru którego należy punkt
, do obszaru którego należy punkt 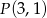 .
.
Wyznacz równanie okręgu przechodzącego przez punkt 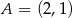 i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Który z odcinków łączących dowolny punkt paraboli o równaniu 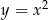 z punktem
z punktem 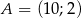 ma najmniejszy kwadrat długości?
ma najmniejszy kwadrat długości?
Wyznacz te punkty paraboli 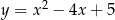 , które znajdują się najbliżej punktu
, które znajdują się najbliżej punktu 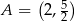 . Oblicz tę najmniejszą odległość.
. Oblicz tę najmniejszą odległość.
Prosta 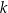 przecina okrąg o środku
przecina okrąg o środku 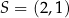 w punktach
w punktach 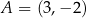 i
i 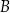 , przy czym
, przy czym 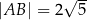 . Wyznacz równanie prostej
. Wyznacz równanie prostej 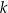 .
.
Okrąg wpisany w trójkąt 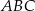 jest opisany równaniem
jest opisany równaniem
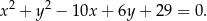
Punkty styczności tego okręgu z bokami 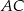 i
i 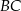 trójkąta
trójkąta 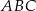 leżą na prostej o równaniu:
leżą na prostej o równaniu: 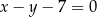 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 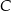 trójkąta
trójkąta 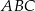 .
.
W okrąg o równaniu 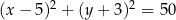 wpisano trójkąt ostrokątny
wpisano trójkąt ostrokątny 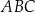 . Bok
. Bok 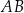 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 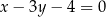 . Wysokość
. Wysokość 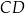 tego trójkąta dzieli bok
tego trójkąta dzieli bok 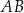 tak, że
tak, że 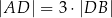 . Oblicz pole trójkąta
. Oblicz pole trójkąta 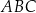 .
.
Punkty 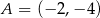 i
i 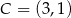 są wierzchołkami rombu
są wierzchołkami rombu 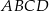 , którego wierzchołek
, którego wierzchołek 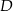 leży na prostej
leży na prostej 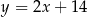 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 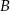 i
i 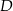 .
.
Dane są punkty 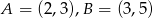 i
i 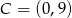 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 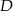 , dla którego czworokąt
, dla którego czworokąt 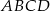 jest trapezem prostokątnym, którego kąt przy wierzchołku
jest trapezem prostokątnym, którego kąt przy wierzchołku 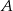 jest prosty.
jest prosty.
Punkty 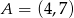 ,
, 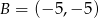 i
i 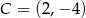 są wierzchołkami trapezu prostokątnego
są wierzchołkami trapezu prostokątnego 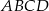 o podstawach
o podstawach 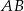 i
i 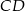 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 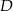 .
.

