Geometria analityczna/Geometria - zadania z matematyki

/Szkoła średnia/Geometria/Geometria analityczna

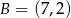Punkt B = (7,2) jest wierzchołkiem trójkąta równoramiennego 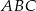ABC o podstawie 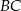. Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka 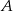tego trójkąta zawiera się w prostej o równaniu 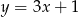y = 3x + 1 . Oblicz współrzędne punktów 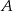i 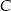. Rozważ wszystkie przypadki.

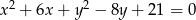Wyznacz równania stycznych do okręgu 2 2 x + 6x + y − 8y + 21 = 0 równoległych do osi .

Ukryj Podobne zadania

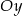Wyznacz równania stycznych do okręgu o równaniu 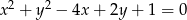2 2 x + y − 4x + 2y + 1 = 0 , równoległych do osi odciętych układu współrzędnych.

Wyznacz równania stycznych do okręgu o równaniu 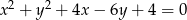2 2 x + y + 4x − 6y + 4 = 0 , równoległych do osi rzędnych układu współrzędnych.

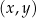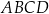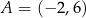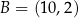W kartezjańskim układzie współrzędnych (x,y ) dany jest równoległobok ABCD , w którym A = (− 2,6) oraz B = (10 ,2 ) . Przekątne 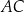oraz 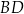tego równoległoboku przecinają się w punkcie 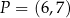P = (6 ,7) . Oblicz długość boku 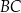tego równoległoboku.

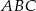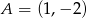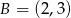Pole trójkąta ABC o danych wierzchołkach A = (1,− 2) oraz B = (2,3) jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu x + y − 2 = 0 .

Ukryj Podobne zadania

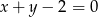Znajdź taki punkt 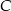, leżący na prostej 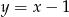y = x − 1 , aby pole trójkąta 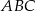ABC , którego wierzchołkami są punkty: 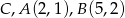C,A (2,1),B (5,2) było równe 5.

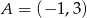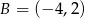Dane są punkty A = (− 1,3) i B = (− 4,2) . Wyznacz współrzędne punktu 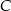na prostej 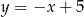y = −x + 5 tak, aby pole trójkąta 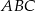ABC było równe 7.

Prosta 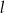, na której leży punkt 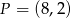P = (8,2) , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej .

Ukryj Podobne zadania

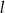Prosta 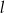, na której leży punkt 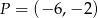P = (−6 ,−2 ) , tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej .

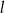W kartezjańskim układzie współrzędnych 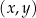(x,y ) trapez 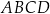ABCD jest wpisany w okrąg o środku w punkcie 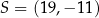S = (19,− 11) i promieniu 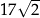√ -- 1 7 2 . Wierzchołek 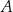trapezu ma obie współrzędne ujemne, a odcinek 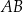jest dłuższą z podstaw tego trapezu. Przekątna 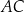trapezu 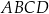ABCD jest zawarta w prostej o równaniu 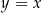y = x . Oblicz sinus kąta ABC .

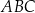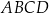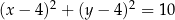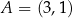Kwadrat ABCD jest wpisany w okrąg o równaniu 2 2 (x − 4 ) + (y − 4) = 10 oraz A = (3,1) . Wyznacz równanie prostej zawierającej przekątną 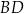tego kwadratu.

Punkt 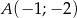A (− 1;− 2) jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej 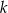o równaniu 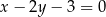x − 2y − 3 = 0 . Środkiem symetrii tego rombu jest punkt 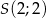S(2;2) . Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.

Punkt 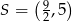( 9 ) S = 2,5 jest środkiem symetrii prostokąta 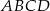ABCD , którego pole jest równe 30, a bok 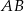jest zawarty w prostej o równaniu 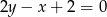2y − x+ 2 = 0 . Oblicz współrzędne wierzchołków prostokąta ABCD .

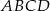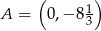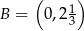Dane są punkty ( 1) A = 0 ,− 8 3 i ( 1) B = 0 ,23 . Wyznacz na prostej 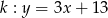k : y = 3x+ 13 punkt 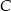, tak aby 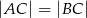|AC | = |BC | . Dla wyznaczonego punktu C:

wykaż, że trójkąt 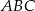jest prostokątny;
wyznacz równanie okręgu opisanego na trójkącie .

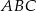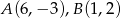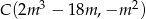Dane są punkty A (6,− 3),B(1,2) oraz 3 2 C (2m − 18m ,−m ) . Wyznacz wszystkie wartości 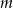, dla których proste 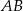i 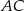są prostopadłe.

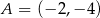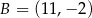Punkty A = (− 2,− 4) i B = (11,− 2) są wierzchołkami trójkąta 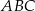ABC . Wierzchołek 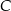tego trójkąta leży na prostej 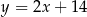y = 2x + 14 , a dwusieczna kąta 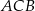ACB przecina bok 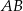w punkcie 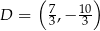( ) D = 7 ,− 10 3 3 . Oblicz współrzędne wierzchołka 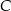trójkąta ABC .

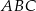Dane są punkty 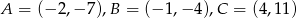A = (− 2,− 7),B = (− 1,− 4),C = (4,11) . Wykaż, że punkty te są współliniowe

Na prostej 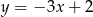y = − 3x+ 2 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.

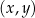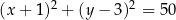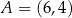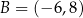W kartezjańskim układzie współrzędnych (x,y ) dane są: okrąg o równaniu (x + 1)2 + (y − 3)2 = 5 0 i punkty A = (6 ,4) oraz B = (− 6,8) . Punkt 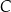leży na tym okręgu i 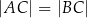|AC | = |BC | . Oblicz współrzędne punktu 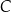. Rozważ wszystkie przypadki.

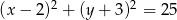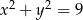Określ wzajemne położenie okręgów 2 2 (x − 2 ) + (y + 3) = 25 i 2 2 x + y = 9 .

Ukryj Podobne zadania

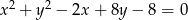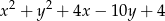Określ wzajemne położenie okręgów 2 2 x + y − 2x + 8y − 8 = 0 i x 2 + y2 + 4x − 1 0y+ 4 .

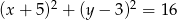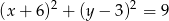Określ wzajemne położenie okręgów: 2 2 (x + 5 ) + (y − 3) = 1 6 i (x + 6)2 + (y − 3)2 = 9 .

Dany jest okrąg 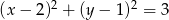2 2 (x− 2) + (y − 1 ) = 3 . Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 60∘ .

Ukryj Podobne zadania

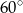Dany jest okrąg 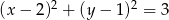2 2 (x− 2) + (y− 1) = 3 . Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 60∘ .

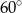Wyznacz współrzędne punktu 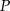leżącego na wykresie funkcji 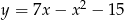2 y = 7x− x − 15 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza.

Dany jest ciąg punktów 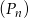(Pn) na płaszczyźnie, których współrzędne dane są wzorem 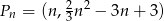Pn = (n, 23n 2 − 3n + 3) , gdzie 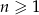n ≥ 1 . Wyznacz tę wartość , dla której odległość punktu 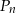od prostej 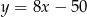y = 8x − 50 jest najmniejsza z możliwych.

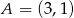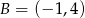Dane są punkty A = (3,1) i B = (− 1,4) oraz prosta 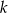o równaniu 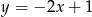y = − 2x+ 1 . Wyznacz taki punkt 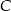prostej 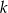, aby suma kwadratów boków trójkąta 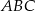ABC była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.

Strona 3 z 27