Wyznacz liczbę  tak, aby liczby dodatnie
tak, aby liczby dodatnie 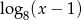 ,
, 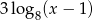 , 6 tworzyły ciąg geometryczny (w podanej kolejności).
, 6 tworzyły ciąg geometryczny (w podanej kolejności).
/Szkoła średnia/Ciągi/Geometryczny/Trzywyrazowy/1 niewiadoma
Liczby 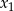 i
i 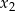 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 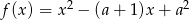 . Dla jakich
. Dla jakich 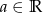 ciąg
ciąg 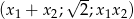 jest geometryczny?
jest geometryczny?
Dla jakich wartości  liczby
liczby 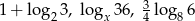 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Dany jest ciąg 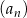 określony wzorem
określony wzorem 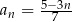 dla każdej liczby naturalnej
dla każdej liczby naturalnej 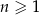 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 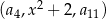 , gdzie
, gdzie  jest liczbą rzeczywistą, jest geometryczny. Oblicz
jest liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.
Dany jest ciąg 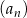 określony wzorem
określony wzorem 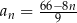 dla każdej liczby naturalnej
dla każdej liczby naturalnej 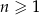 . Trójwyrazowy ciąg
. Trójwyrazowy ciąg 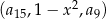 , gdzie
, gdzie  jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz
jest dodatnią liczbą rzeczywistą, jest geometryczny. Oblicz  oraz iloraz tego ciągu geometrycznego.
oraz iloraz tego ciągu geometrycznego.
Wyznacz wszystkie wartości 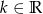 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 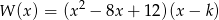 są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
Wyznacz wszystkie wartości  , dla których trzy liczby:
, dla których trzy liczby: 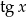 ,
, 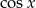 ,
, 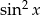 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
Wyznacz  tak, aby ciąg
tak, aby ciąg 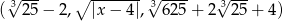 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Funkcja 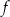 jest określona wzorem
jest określona wzorem 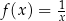 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 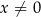 . Oblicz wartość
. Oblicz wartość 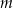 , dla której liczby
, dla której liczby 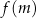 ,
, 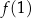 ,
, 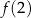 są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
Jaką liczbą musi być  , aby liczby:
, aby liczby: 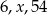 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Wyznacz wszystkie wartości  , gdzie
, gdzie 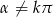 ,
, 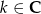 , dla których trzy liczby
, dla których trzy liczby 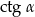 ,
, 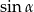 ,
, 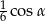 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
Dla jakich liczb 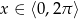 liczby
liczby 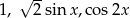 są trzema kolejnymi wyrazami ciągu geometrycznego?
są trzema kolejnymi wyrazami ciągu geometrycznego?
Wyznacz liczbę  , tak aby liczby dodatnie:
, tak aby liczby dodatnie: 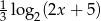 ,
, 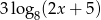 ,
, 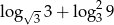 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Dla jakich 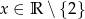 , liczby
, liczby 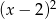 ,
, 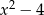 ,
, 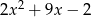 w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości
w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości  wyznacz ciąg i jego iloraz.
wyznacz ciąg i jego iloraz.
Wiadomo, że liczby 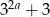 ,
, 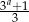 ,
, 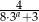 są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz
są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz  . Dla wyznaczonej wartości
. Dla wyznaczonej wartości  zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
Liczby 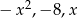 w podanej kolejności tworzą ciąg geometryczny. Oblicz
w podanej kolejności tworzą ciąg geometryczny. Oblicz  .
.
Liczby 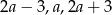 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 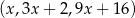 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 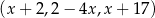 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 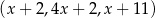 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Rozwiąż układ równań:
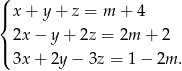
Dla jakich wartości parametru 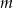 liczby
liczby 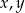 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Ciąg 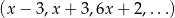 jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że
jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że 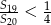 , gdzie
, gdzie 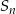 oznacza sumę
oznacza sumę  początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu.

