Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.
/Szkoła średnia/Ciągi/Arytmetyczny/Różne
Wyrazami ciągu arytmetycznego 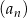 są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto 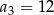 . Oblicz
. Oblicz 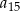 .
.
Wyrazami ciągu arytmetycznego 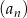 są kolejne liczby naturalne, które przy dzieleniu przez 8 dają resztę 5. Wyraz pierwszy jest mniejszy od 8. Oblicz
są kolejne liczby naturalne, które przy dzieleniu przez 8 dają resztę 5. Wyraz pierwszy jest mniejszy od 8. Oblicz 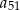 .
.
Wyrazami ciągu arytmetycznego 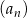 są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 3. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 3. Ponadto 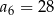 . Oblicz
. Oblicz 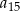 .
.
Wyrazami ciągu arytmetycznego 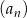 są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto 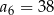 . Oblicz
. Oblicz 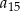 .
.
W ciągu arytmetycznym 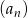 o różnicy
o różnicy 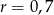 dany jest wyraz
dany jest wyraz 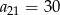 . Oblicz
. Oblicz 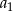 oraz sumę 21 początkowych wyrazów ciągu
oraz sumę 21 początkowych wyrazów ciągu 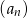 .
.
Różnica ciągu arytmetycznego jest równa 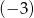 , a szósty wyraz jest równy 3012. Oblicz sumę 2017 początkowych wyrazów tego ciągu.
, a szósty wyraz jest równy 3012. Oblicz sumę 2017 początkowych wyrazów tego ciągu.
Ciąg 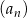 jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym
jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym 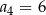 . Ciąg
. Ciąg 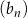 dla dowolnego
dla dowolnego 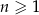 spełnia warunek
spełnia warunek 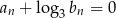 . Oblicz granicę
. Oblicz granicę
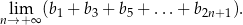
Iloczyn pierwszego i piątego wyrazu malejącego ciągu arytmetycznego 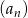 jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
Iloczyn pierwszego i czwartego wyrazu malejącego ciągu arytmetycznego 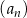 jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
Pierwszy wyraz ciągu arytmetycznego 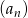 wynosi 1. Dla jakiej wartości różnicy
wynosi 1. Dla jakiej wartości różnicy  wyrażenie
wyrażenie 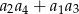 ma wartość najmniejszą i ile ona wynosi?
ma wartość najmniejszą i ile ona wynosi?
Ciąg 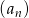 jest ciągiem arytmetycznym o różnicy 2, a ciąg
jest ciągiem arytmetycznym o różnicy 2, a ciąg 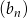 zdefiniowany jest wzorem
zdefiniowany jest wzorem 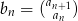 , dla
, dla 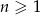 . Wyznacz wartość
. Wyznacz wartość  , dla której
, dla której 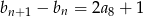 .
.
Ciąg 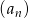 jest ciągiem arytmetycznym, w którym
jest ciągiem arytmetycznym, w którym 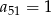 oraz wyrażanie
oraz wyrażanie 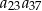 ma najmniejszą możliwą wartość. Wyznacz
ma najmniejszą możliwą wartość. Wyznacz 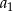 .
.
Wartość pewnej frezarki maleje z roku na rok. Wartości tej frezarki w kolejnych latach tworzą ciąg arytmetyczny. Oblicz czas, w ciągu którego frezarka całkowicie straci wartość (zamortyzuje się), jeżeli wiadomo, że po 15 latach użytkowania jej wartość była 3 razy większa niż jej wartość po 25 latach.
Wszystkie liczby parzyste z przedziału 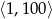 , które nie są podzielne przez 4 ustawiamy w ciąg
, które nie są podzielne przez 4 ustawiamy w ciąg 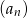 .
.
- Wyznacz wzór ciągu
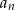 i uzasadnij, że jest on arytmetyczny.
i uzasadnij, że jest on arytmetyczny. - Oblicz sumę wszystkich wyrazów tego ciągu.

