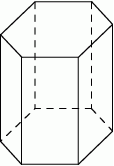
Wielokąt wypukły ma  wierzchołków,
wierzchołków, 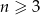 ,
, 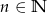 , spośród których losujemy jednocześnie dwa. Wyznacz
, spośród których losujemy jednocześnie dwa. Wyznacz  , wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od
, wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od 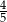 .
.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Geometryczne
Z sześciu odcinków długości 1,3,5,6,7,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo że można z nich zbudować trójkąt.
Losujemy dwa różne punkty spośród wierzchołków sześcianu o boku długości 1. Jakie jest prawdopodobieństwo, że
- odległość wylosowanych wierzchołków jest równa 1?
- odległość wylosowanych wierzchołków jest większa od
 ?
?
Umieszczamy króla szachowego w lewym dolnym rogu 64-polowej szachownicy, a następnie siedem razy przesuwamy go losowo w górę lub w prawo (za każdym razem na nowo losujemy kierunek przesunięcia).

Zakładając, że wylosowanie każdego kierunku jest jednakowo prawdopodobne, oblicz prawdopodobieństwo, że na końcu król nie znajdzie się w rogu szachownicy.
Jakie jest prawdopodobieństwo tego, że losowo wybrane 4 różne wierzchołki sześcianu są wierzchołkami czworościanu foremnego?
Oblicz prawdopodobieństwo tego, że trzy losowo wybrane wierzchołki sześcianu są wierzchołkami trójkąta równobocznego.
Rozważmy zbiór wszystkich czteroelementowych podzbiorów zbioru wierzchołków pewnego prostopadłościanu. Oblicz prawdopodobieństwo wylosowania takiego podzbioru, którego elementy są wierzchołkami prostokąta.
Na osi liczbowej każde dwie spośród 1000 kolejnych liczb naturalnych 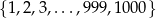 połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
Sześcian pomalowano, a następnie rozcięto na 1000 jednakowych sześcianików, które wrzucono do pudełka i wymieszano. Oblicz prawdopodobieństwo wylosowania z tego pudełka jednego, który:
- będzie miał dwie ściany pomalowane;
- będzie miał trzy ściany pomalowane;
- będzie miał jedną lub dwie ściany pomalowane.
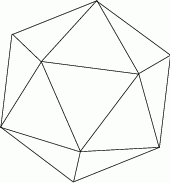
Każda ściana dwudziestościanu foremnego 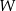 jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu
jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu 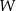 . Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu
. Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu 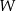 ?
?
Oblicz prawdopodobieństwo tego, że dwa losowo wybrane wierzchołki sześciokąta foremnego o boku długości 1, są końcami odcinka o długości 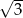 .
.
Na diagramie składającym się z 9 kwadratowych pól w układzie 3x3 zaznaczono w losowo wybranych polach kółko i krzyżyk. Jakie jest prawdopodobieństwo tego, że oba znaki znalazły się na sąsiednich polach tzn. stykających się jednym bokiem.
Ze zbioru punktów o współrzędnych 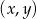 , gdzie
, gdzie 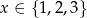 zaś
zaś 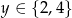 wybrano losowo dwa różne punkty. Oblicz prawdopodobieństwa zdarzeń:
wybrano losowo dwa różne punkty. Oblicz prawdopodobieństwa zdarzeń:
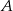 – wylosowane punkty należą do prostej o równaniu
– wylosowane punkty należą do prostej o równaniu 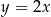 ;
; 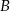 – wylosowane punkty są końcami odcinka równoległego do osi
– wylosowane punkty są końcami odcinka równoległego do osi 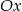 .
.
Każdą krawędź sześcianu kolorujemy jednym z 6 kolorów, wśród których są kolory: biały i czarny. Oblicz prawdopodobieństwo, że wśród pokolorowanych krawędzi są dokładnie 3 krawędzie białe i 2 czarne. Wynik podaj w postaci ułamka nieskracalnego.
Sześcian, którego ściany zostały pomalowane czerwoną farbą, dzielimy 6 płaszczyznami równoległymi do jego ścian na 27 identycznych sześcianików. Losujemy 2 spośród nich.
- Oblicz prawdopodobieństwo, że łączna liczba czerwonych ścian wylosowanych sześcianików wynosi 3.
- Oblicz prawdopodobieństwo, że wylosowane sześcianiki mają wspólną ścianę.
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.